En este post se explica qué son los polígonos semejantes y cuáles son sus características. Además, podrás ver un ejemplo resuelto de la semejanza de polígonos para acabar de entender el concepto.
Índice
¿Qué son los polígonos semejantes?
Los polígonos semejantes son aquellos polígonos que tienen la misma forma aunque tengan diferente tamaño. Por lo tanto, dos polígonos son semejantes si son proporcionales, es decir, si tienen los lados correspondientes proporcionales y los ángulos correspondientes iguales.
Así pues, dos polígonos semejantes pueden tener lados diferentes, pero si tienen exactamente la misma forma se consideran semejantes.
De hecho, si se multiplican todos los lados de un polígono por un mismo valor, se obtiene un polígono semejante a él.
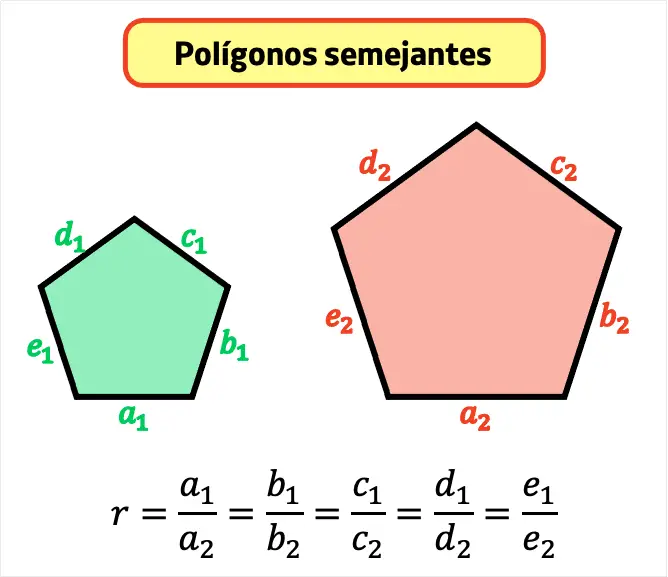
Se dice razón de semejanza al valor de la proporción entre los lados de dos polígonos semejantes, y suele expresarse con la letra r.
Propiedades de los polígonos semejantes
Las propiedades de los triángulos semejantes son:
- Propiedad reflexiva: todo polígono es semejante a sí mismo.
- Propiedad idéntica o simétrica: si un polígono es semejante a otro, el segundo polígono también es semejante al primero.
- Propiedad transitiva: si un polígono es semejante a otro y al mismo tiempo el segundo polígono es semejante a un tercer polígono, el primer y el tercer polígono también son semejantes entre sí.
- Todos los polígonos regulares que tienen el mismo número de lados son semejantes entre sí.
- Dados dos polígonos semejantes, el perímetro de un polígono es equivalente al perímetro del otro triángulo multiplicado por la razón de semejanza.
- Si dos polígonos son semejantes, el área de un polígono es igual al área del otro polígono multiplicado por el cuadrado de la razón de semejanza.
Ejercicio resuelto de polígonos semejantes
- Sabiendo que todos los ángulos correspondientes de los siguientes dos polígonos irregulares son idénticos, determina si son semejantes o no.
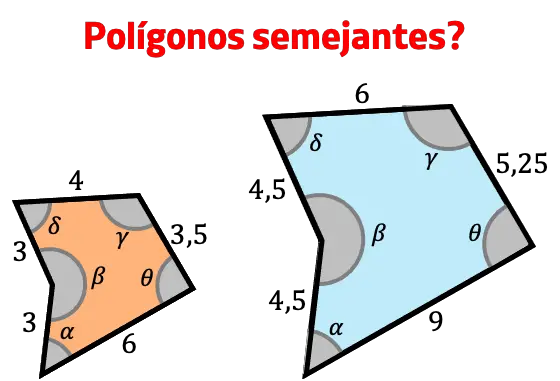
Para determinar si los dos polígonos son semejantes primero tenemos que ver si los lados son proporcionales, así que dividimos los lados correspondientes:
Hemos obtenido el mismo resultado de todas las divisiones, por lo que los lados de los polígonos son proporcionales. No obstante, este no es un criterio suficiente para determinar que los polígonos son semejantes, también es necesario que sus ángulos sean iguales.
Pero como el enunciado del problema nos dice que sus ángulos son los mismos, podemos concluir que son dos polígonos semejantes porque todos sus lados son proporcionales y además sus ángulos son iguales.
Asimismo, la razón de semejanza de estos polígonos semejantes es de 1,5.
Polígonos semejantes y polígonos congruentes
Por último, veremos cuál es la diferencia entre los polígonos semejantes y los polígonos congruentes, ya que son dos tipos de polígonos que se suelen confundir.
Los polígonos congruentes son aquellos que tienen la misma forma y tamaño, es decir, dos polígonos son congruentes si todos sus lados y ángulos correspondientes son iguales.
Por lo tanto, la diferencia entre los polígonos semejantes y los polígonos congruentes es que los polígonos semejantes tienen los lados proporcionales y los ángulos iguales, mientras que los polígonos congruentes tienen los lados y los ángulos iguales.
