En este artículo se explica qué son los triángulos semejantes y cuáles son sus características. También encontrarás cómo determinar si dos triángulos son semejantes y, además, podrás practicar con un ejemplo resuelto paso a paso.
Índice
¿Qué son los triángulos semejantes?
Los triángulos semejantes son aquellos triángulos que tienen los mismos ángulos. Por lo tanto, dos triángulos son semejantes si tienen la misma forma, aunque tengan diferente tamaño.
Es decir, dos triángulos semejantes pueden tener lados diferentes, pero si tienen exactamente la misma forma se consideran semejantes.
De hecho, si se multiplican las longitudes de los lados de un triángulo por un valor constante, se obtiene un triángulo semejante a él.
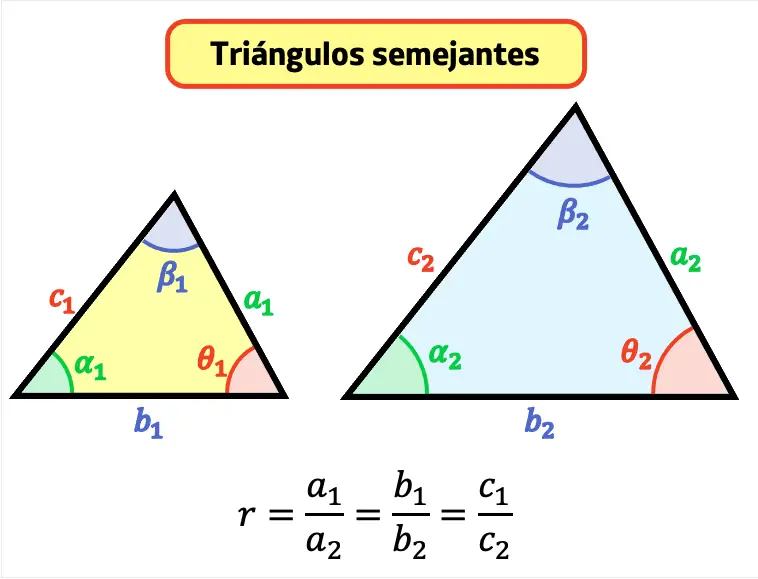
Se dice razón de semejanza al valor de la proporción entre los lados de dos triángulos semejantes. La razón de semejanza de dos triángulos se suele expresar con la letra r.
Criterios de semejanza de triángulos
Los criterios para identificar si dos o más triángulos son semejantes son los siguientes:
- Criterio de semejanza 1: dos triángulos son semejantes si tienen dos ángulos iguales.
- Criterio de semejanza 2: dos triángulos son semejantes si tienen dos lados proporcionales y además los ángulos comprendidos entre ellos son iguales.
- Criterio de semejanza 3: dos triángulos son semejantes si tienen los tres lados proporcionales.
Propiedades de los triángulos semejantes
Las propiedades de los triángulos semejantes son:
- Propiedad reflexiva: todo triángulo es semejante a sí mismo.
- Propiedad idéntica o simétrica: si un triángulo es semejante a otro, el segundo triángulo también es semejante al primero.
- Propiedad transitiva: si un triángulo es semejante a otro y al mismo tiempo el segundo triángulo es semejante a un tercer triángulo, el primer y el tercer triángulo también son semejantes entre sí.
- Todos los triángulos equiláteros son semejantes entre sí, ya que todos los ángulos de cualquier triángulo equilátero miden lo mismo.
- Dados dos triángulos semejantes, el perímetro de un triángulo es equivalente al perímetro del otro triángulo multiplicado por la razón de semejanza.
- Si dos triángulos son semejantes, el área de un triángulo es igual al área del otro triángulo multiplicado por el cuadrado de la razón de semejanza.
Ejercicio resuelto de triángulos semejantes
- Determina si los siguientes triángulos son semejantes y, en tal caso, calcula la razón de semejanza.

En este caso sabemos cuánto miden todos los lados de los dos triángulos y no conocemos el valor de ningún ángulo, por lo que debemos aplicar el tercer criterio de la semejanza de triángulos.
Así pues, tenemos que comprobar si los lados de los triángulos son proporcionales. Para ello, dividimos los lados similares para ver si obtenemos el mismo valor:
Como el resultado de las tres divisiones es equivalente, significa que los lados de los triángulos son proporcionales. Por lo tanto, los triángulos del ejercicio son semejantes.
Además, la razón de semejanza de los dos triángulos es el cociente entre las longitudes de sus lados, que en este caso es 0,8.

