En este artículo encontrarás cuáles son todas las propiedades de los triángulos. Te explicamos cada propiedad de los triángulos detalladamente y, además, podrás ver ejemplos de las aplicaciones de las propiedades de los triángulos.
Índice
¿Cuáles son las propiedades de los triángulos?
Propiedad 1: suma de los ángulos interiores
La suma de todos los ángulos internos de cualquier triángulo siempre da como resultado 180º.
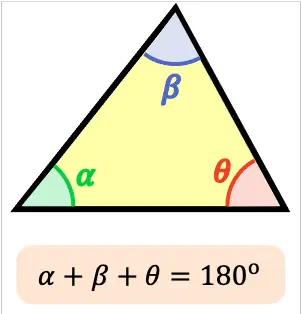
Esta propiedad de los triángulos resulta muy útil para calcular cuánto mide un ángulo del triángulo cuando ya se conocen los valores de los otros dos ángulos.
Propiedad 2: valor de un ángulo exterior
En todos los triángulos se cumple que el valor de un ángulo exterior es igual a la suma de los ángulos interiores no adyacentes.
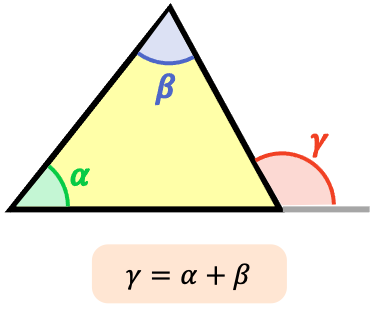
Esta propiedad se puede deducir de la propiedad anterior y de la condición de que un ángulo interior más su correspondiente ángulo exterior suman 180º.
Propiedad 3: suma de los ángulos exteriores
Para cualquier triángulo, la suma de los ángulos exteriores es equivalente a 360º.
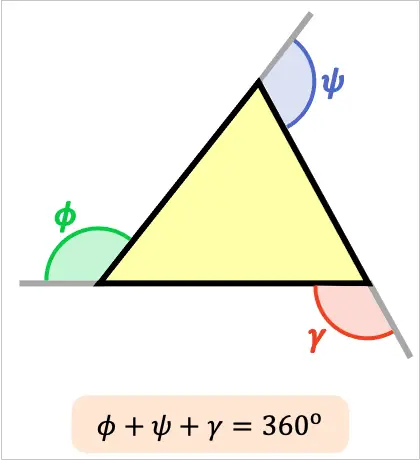
Por lo tanto, la suma de los ángulos exteriores de un triángulo es el doble que la suma de los ángulos interiores de ese mismo triángulo.
Propiedad 4: relación de los lados con los ángulos
Cuanto mayor sea el lado de un triángulo, mayor será su ángulo opuesto.
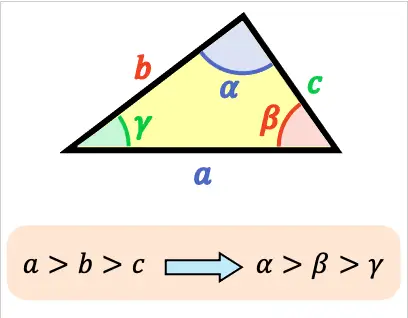
Por lo tanto, si un triángulo tiene dos lados iguales, sus ángulos opuestos también serán iguales. Este es el caso del triángulo isósceles.
Propiedad 5: longitud de un lado
En cualquier triángulo se cumple que la longitud de un lado es mayor que la diferencia positiva de los otros dos lados y, asimismo, es menor que la suma de los otros dos lados.
Por lo tanto, si ,
y
son los tres lados del triángulo, se cumplen las siguientes inecuaciones:
Propiedad 6: triangulación de polígonos
Cualquier polígono se puede descomponer en triángulos, de manera que una figura geométrica plana se puede dividir en múltiples triángulos más pequeños. A este proceso se llama triangulación de un polígono.
Aunque lógicamente la triangulación del polígono se puede hacer con triángulos de varias formas, lo más fácil es aprovechar las diagonales del polígono.
Por ejemplo, un hexágono regular puede descomponerse en seis triángulos equiláteros.
Propiedad 7: diagonales de un triángulo
Una diagonal de un polígono es un segmento que une dos vértices del polígono no consecutivos.
Por lo tanto, un triángulo no tiene ninguna diagonal, ya que el segmento que une dos vértices no consecutivos se trata de un lado del triángulo.
Así pues, el triángulo es el único polígono que no tiene ninguna diagonal.
Propiedad 8: teorema de Pitágoras
En los triángulos rectángulos, se cumple que el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos del triángulo.
Esta propiedad de los triángulos se conoce como teorema de Pitágoras.
