En este post te explicamos cuáles son los diferentes criterios de congruencia de triángulos. Además, podrás practicar los conceptos explicados con un ejercicio resuelto de los criterios de congruencia de triángulos.
Índice
¿Cuáles son los criterios de congruencia de triángulos?
Los criterios de congruencia de triángulos son:
- Criterio 1 (LLL): dos triángulos son congruentes si todos sus lados son iguales.
- Criterio 2 (LAL): dos triángulos son congruentes si tienen dos lados y los ángulos comprendidos entre ellos iguales.
- Criterio 3 (ALA): dos triángulos son congruentes si tienen un lado y sus dos ángulos adyacentes iguales.
A continuación se explican los diferentes criterios de congruencia detalladamente y se muestra un ejemplo de cada criterio.
Primer criterio de congruencia (LLL)
El criterio de congruencia de triángulos lado, lado, lado (LLL) dice que dos triángulos son congruentes si tienen sus tres lados iguales.
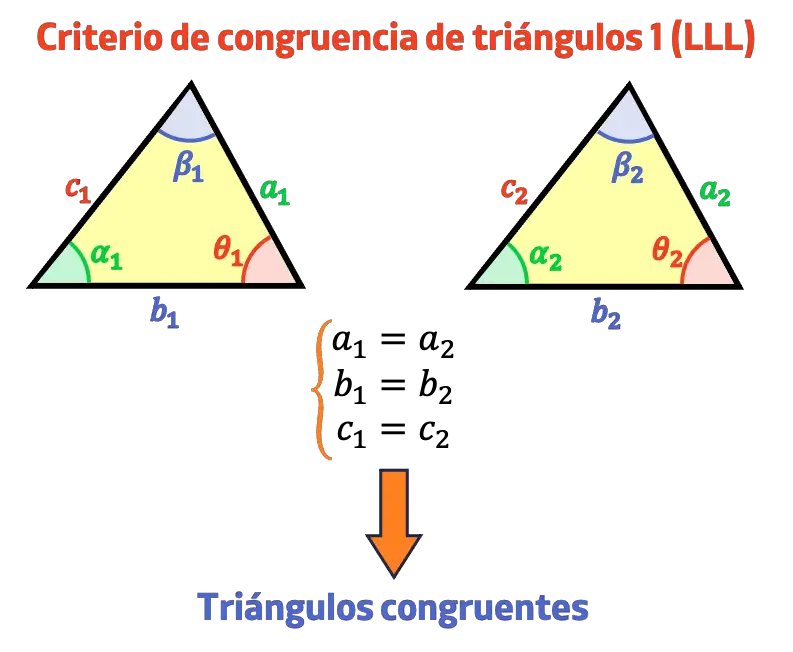
Este criterio no puede utilizarse con los ángulos, pues si dos triángulos tienen todos los ángulos iguales significa que son semejantes, pero no implica que sean congruentes.
Segundo criterio de congruencia (LAL)
El criterio de congruencia de triángulos lado, ángulo, lado (LAL) establece que si dos triángulos tienen dos lados correspondientes iguales y, además, sus ángulos comprendidos entre esos lados también son iguales, significa que los triángulos son congruentes.
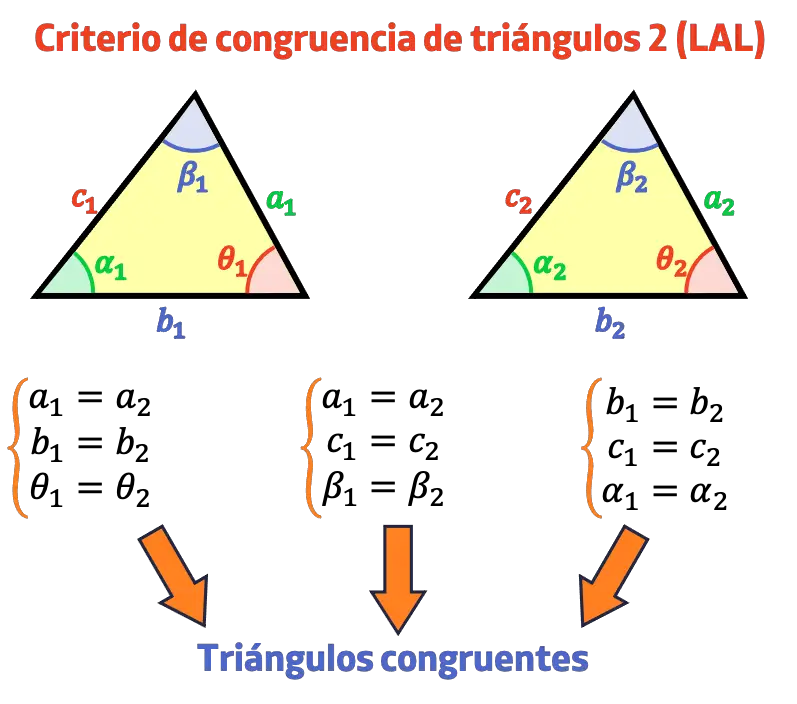
Dos lados de un triángulo junto con el ángulo que forman definen el triángulo completamente, por lo que pueden usarse como criterio de congruencia.
Tercer criterio de congruencia (ALA)
El criterio de congruencia ángulo, lado, ángulo (ALA) dice que dos triángulos son congruentes si tienen dos ángulos iguales y el lado entre esos ángulos también es igual.
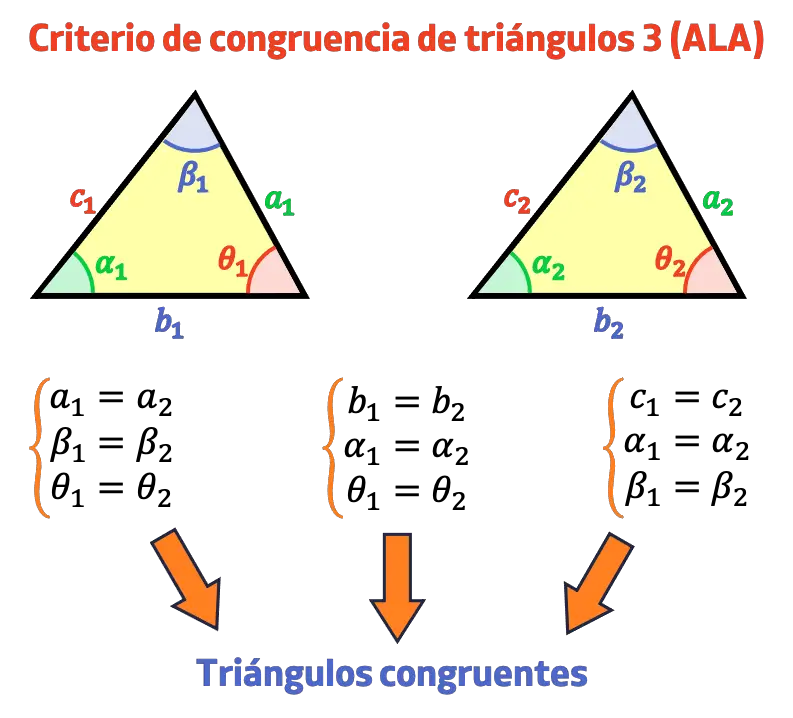
Ejercicio resuelto de los criterios de congruencia de triángulos
- Dado el siguiente heptágono regular, determina si los triángulos GFA y FEG son congruentes.
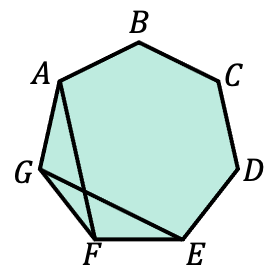
Como la figura geométrica del ejercicio es un heptágono regular, significa que todos sus lados son iguales. Por lo tanto, los lados AG, GF y FE de los triángulos miden lo mismo.
Además, otra característica de los polígonos regulares es que todos sus ángulos interiores son iguales, de modo que el ángulo formado por los lados AG y GF y el ángulo formado por los lados GF y FE son idénticos.
Así pues, gracias al criterio de congruencia de triángulos lado, ángulo, lado (LAL) sabemos que los dos triángulos son congruentes, porque tienen dos lados iguales y los ángulos entre esos lados también son iguales.
