En este post te explicamos qué son los triángulos oblicuángulos, cuáles son sus características y cuáles son los tipos de triángulos oblicuángulos. También te mostramos cómo resolver un triángulo oblicuángulo y, además, podrás ver un ejemplo resuelto paso a paso.
Índice
¿Qué es un triángulo oblicuángulo?
Un triángulo oblicuángulo es un triángulo que no tiene ningún ángulo recto (90º). Es decir, un triángulo es oblicuángulo cuando todos sus ángulos interiores son agudos o obtusos.
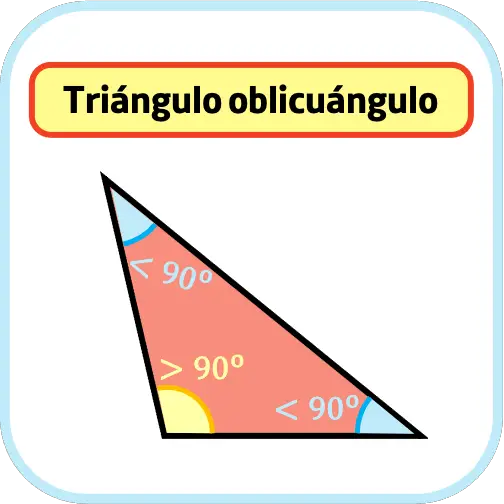
Por lo tanto, la diferencia entre un triángulo oblicuángulo y un triángulo rectángulo es que un triángulo oblicuángulo no tiene ningún ángulo que mida 90º, mientras que un triángulo rectángulo siempre tiene un ángulo recto.
Tipos de triángulo oblicuángulo
Los tipos de triángulo oblicuángulo son:
- Acutángulo: todos los ángulos del triángulo oblicuángulo miden menos de 90º (ángulos agudos).
- Obtusángulo: el triángulo oblicuángulo tiene un ángulo mayor que 90º (ángulo obtuso).
Aunque generalmente los triángulos oblicuángulos se clasifican según si son acutángulos o obtusángulos, también se pueden clasificar según el número de lados iguales. De esta forma se distinguen tres tipos de triángulos oblicuángulos: los triángulos equiláteros, los triángulos isósceles y los triángulos escalenos. Puedes ver en qué consiste cada tipo de triángulo aquí:
Perímetro de un triángulo oblicuángulo
Las longitudes de los lados de un triángulo oblicuángulo pueden ser cualesquiera, de manera que puede tener tres lados iguales, solo dos lados iguales o todos los lados diferentes.
Por lo tanto, no existe una fórmula concreta del perímetro de un triángulo oblicuángulo, sino que para calcular el perímetro de un triángulo oblicuángulo se deben sumar las longitudes de sus tres lados.
Área de un triángulo oblicuángulo
La fórmula de Herón permite calcular la altura de cualquier tipo de triángulo sin conocer su altura, aunque para poder usarla debes saber la longitud de todos los lados de la figura. Por lo tanto, podemos emplear esta fórmula para determinar el área de un triángulo oblicuángulo sin necesidad de hallar su altura.
La fórmula de Herón dice que para hallar el área de un triángulo oblicuángulo se debe calcular la raíz cuadrada del producto del semiperímetro por la diferencia del semiperímetro y la longitud de cada lado del triángulo oblicuángulo.
Donde 
, 
y 
es la longitud de cada lado del triángulo y 
el semiperímetro del triángulo.
Recuerda que el semiperímetro es la semisuma de todos los lados de una figura plana:
Leyes de los triángulos oblicuángulos
A menudo nos encontramos con problemas en los que debemos resolver triángulos oblicuángulos, es decir, tenemos que determinar todos sus lados y todos sus ángulos.
Así pues, a continuación veremos dos leyes matemáticas que te ayudarán a resolver ejercicios de triángulos oblicuángulos.
Ley de los senos
La ley de los senos, o teorema del seno, dice que la proporción entre las longitudes de los lados de un triángulo oblicuángulo y los senos de sus correspondientes ángulos es constante.
Por lo tanto, la fórmula de la ley de los senos es la siguiente:
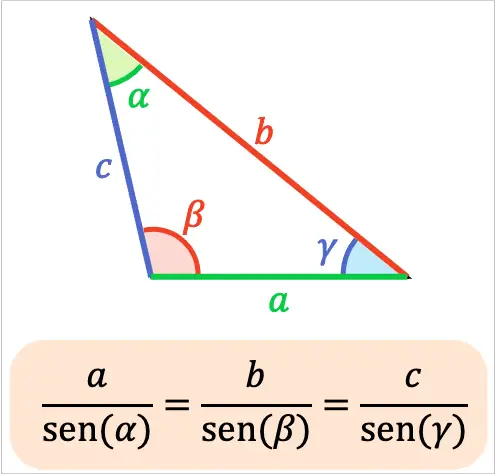
La ley de los senos es útil para determinar el lado de un triángulo oblicuángulo cuando se conoce su ángulo y otro lado junto con su ángulo correspondiente. Asimismo, también puede utilizarse cuando se saben las longitudes de dos lados pero solo uno de sus ángulos.
Ley de cosenos
La ley de cosenos, o teorema del coseno, permite relacionar matemáticamente cualquier lado de un triángulo con los otros dos lados y con el ángulo formado por estos dos últimos lados.
En concreto, la fórmula de la ley de cosenos es la siguiente:
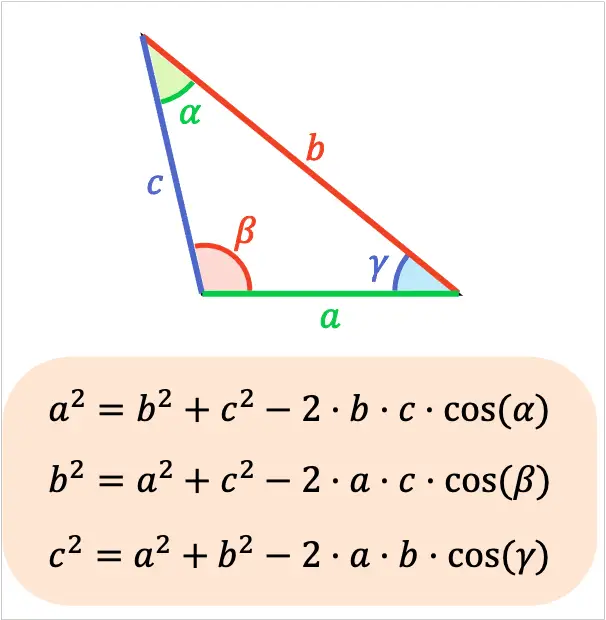
La ley de cosenos resulta muy útil para calcular la longitud de un lado de un triángulo oblicuángulo cuando se conocen los otros dos lados y el ángulo opuesto al lado desconocido.
Ejercicio resuelto de un triángulo oblicuángulo
- Resuelve el siguiente triángulo oblicuángulo:
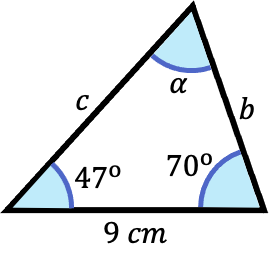
En este caso conocemos dos ángulos del triángulo oblicuángulo. Gracias a las propiedades de los triángulos, sabemos que la suma de todos sus ángulos interiores es 180º. Por lo tanto, podemos hallar el ángulo que nos queda haciendo una resta:
Ahora podemos determinar un lado del triángulo oblicuángulo aplicando la ley de los senos con el lado conocido, el ángulo calculado, otro lado y su ángulo opuesto:
Luego calculamos la longitud del lado restante utilizando la ley del coseno:
De este modo ya hemos conseguido resolver el triángulo oblicuángulo, pues hemos hallado todos sus lados y todos sus ángulos. Ahora también podemos calcular su perímetro sumando todos sus lados:
Y, por último, sacamos el área del triángulo oblicuángulo aplicando la fórmula de Herón:
![\begin{aligned}A&=\sqrt{s(s-a)(s-b)(s-c)}\\[2ex]A&=\sqrt{12,94(12,94-9)(12,94-7,39)(12,94-9,49)}\\[2ex]A&=31,24\end{aligned}](https://www.areasyvolumenes.net/wp-content/ql-cache/quicklatex.com-56cd0b128767dac4bc15fc8852ba535a_l3.svg "Rendered by QuickLaTeX.com")
