En este post te explicamos las diagonales de un rombo, cuáles son sus propiedades, y cómo se calcula el área y el perímetro de un rombo con sus diagonales.
Índice
¿Qué son las diagonales de un rombo?
Las diagonales de un rombo son los segmentos que unen dos vértices no consecutivos del rombo. Por lo tanto, un rombo tiene dos diagonales perpendiculares entre sí.
Las diagonales de un rombo definen las dimensiones de un rombo, es decir, conociendo las longitudes de las dos diagonales del rombo se pueden encontrar todas las características geométricas del rombo.
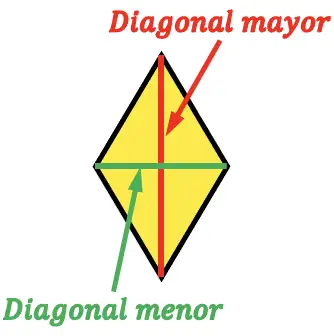
Un rombo puede tener las dos diagonales iguales o puede que una diagonal sea más grande que la otra. En tal caso, se dice diagonal mayor a la diagonal más larga y diagonal menor a la diagonal más pequeña.
Propiedades de las diagonales de un rombo
Las propiedades de las diagonales de un rombo son:
- Una diagonal de un rombo une dos vértices opuestos, o dicho de otra forma, une dos aristas no consecutivas.
- Las dos diagonales de un rombo son rectas perpendiculares entre sí, es decir, entre ellas forman cuatro ángulo de 90 grados.
- Las diagonales del rombo son bisectrices de sus ángulos.
- Cada diagonal de un rombo es un eje de simetría.
- El punto de intersección de las dos diagonales es el incentro del rombo.
- Una diagonal de un rombo divide justo por la mitad a la otra diagonal del rombo.
- Las diagonales de un rombo y sus lados están relacionadas matemáticamente por el teorema de Pitágoras.
Cómo calcular las diagonales de un rombo
Conociendo la longitud de una diagonal y de un lado del rombo, se puede calcular la otra diagonal del rombo utilizando el teorema de Pitágoras.
Las dos diagonales de cualquier rombo dividen a esta figura geométrica en cuatro triángulos rectángulos, por tanto, se puede hallar la longitud de una diagonal usando el teorema de Pitágoras.
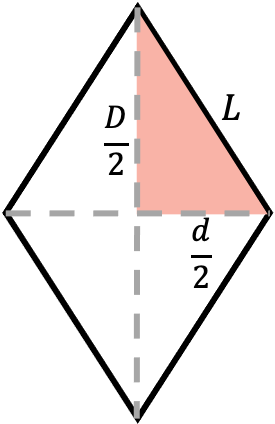
De manera que la longitud de un lado del rombo elevado al cuadrado es equivalente a la suma de cuadrados de las dos semidiagonales del rombo.
Por ejemplo, si sabemos que la diagonal menor de un rombo mide 10 cm y sus lados 13 cm, podemos sacar la longitud de la otra diagonal del rombo despejando la incógnita de la fórmula anterior.
En conclusión, la diagonal mayor del rombo mide 24 cm.
Calcular el área de un rombo con sus diagonales
Ahora que ya hemos visto la definición de las diagonales de un rombo, vamos a profundizar más en el concepto y ver para qué sirven. Porque las diagonales de este tipo de paralelogramo se utilizan para hallar el área y el perímetro del rombo.
Las diagonales de un rombo sirven para calcular el área del rombo. El área de un rombo es igual a la diagonal mayor del rombo por la diagonal menor del rombo partido por dos.
Por ejemplo, calcularemos el área del siguiente rombo cuya diagonal mayor mide 5 cm y la diagonal menor 3 cm.
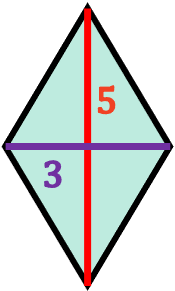
Para hallar el área del rombo se multiplican sus diagonales y luego se divide entre dos.
Ahora sustituimos el valor de las diagonales del rombo en la fórmula y hacemos el cálculo de su área:
Calcular el perímetro de un rombo con sus diagonales
Las diagonales de un rombo también se usan para calcular el perímetro de un rombo.
Para calcular el perímetro de un rombo conociendo sus diagonales debemos multiplicar dos por la raíz cuadrada de la suma de los cuadrados de las diagonales.
Siguiendo el ejemplo del rombo anterior, el cálculo de su perímetro sería:
Sin embargo, el perímetro de un rombo se puede calcular de una manera más fácil. Haz click en el siguiente enlace para ver cómo se hace.
