Te explicamos cómo se calcula el área de un rombo. Encontrarás cuál es la fórmula del área de un rombo y, además, calculamos varios ejemplos de áreas de rombos.
Índice
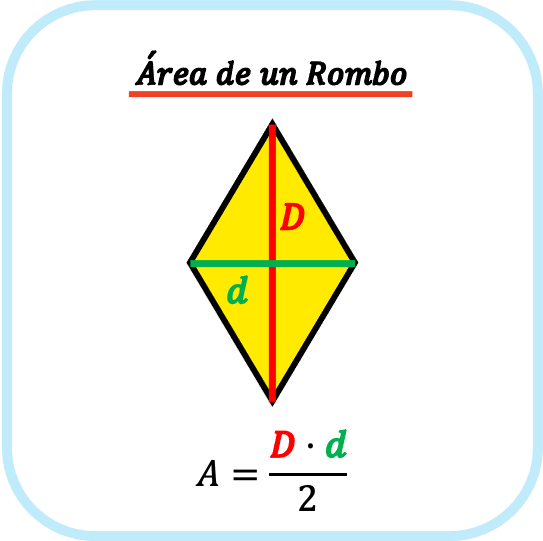
Fórmula del área de un rombo
El área de un rombo es igual a la diagonal mayor del rombo por la diagonal menor del rombo dividido entre dos.
👉 Puedes usar la calculadora que hay más abajo para calcular el área de cualquier rombo.
Por tanto, el área de un rombo se calcula a partir de sus diagonales.
El cálculo del área de un rombo es una característica de esta figura geométrica que lo diferencia de los demás paralelogramos, ya que el área del cuadrado, del rectángulo y del romboide se halla multiplicando su base por su altura. En cambio, para calcular el área de un rombo se debe multiplicar sus diagonales y luego dividir entre dos.
Ejemplo del área de un rombo
Una vez sabemos cuál es la fórmula del área de un rombo, en este apartado calcularemos el área de este tipo de paralelogramo a modo de ejemplo. De este modo te resultará más fácil entender cómo se saca el área de un rombo.
- Calcula el área del rombo cuya diagonal mayor mide 5 cm y la diagonal menor 3 cm.
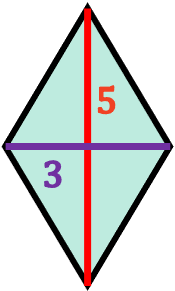
Para hallar el área del rombo se multiplican sus diagonales y luego se divide entre dos.
Ahora sustituimos el valor de las diagonales del rombo en la fórmula y hacemos el cálculo de su área:
Calculadora del área y del perímetro de un rombo
Introduce las longitudes de las diagonales del rombo en la siguiente calculadora online para calcular su área y su perímetro. Debes introducir los números en centímetros utilizando el punto como separador decimal.
Ejercicios resueltos del área de un rombo
Ejercicio 1
Halla el área del rombo cuyas diagonales miden 11 cm y 7 cm.
Para encontrar el área del rombo debemos aplicar su fórmula correspondiente:
Entonces, tenemos que calcular la mitad del producto de las diagonales del rombo para sacar su área:
Ejercicio 2
Calcula el área de un rombo que está inscrito en un cuadrado de lado 6 cm.
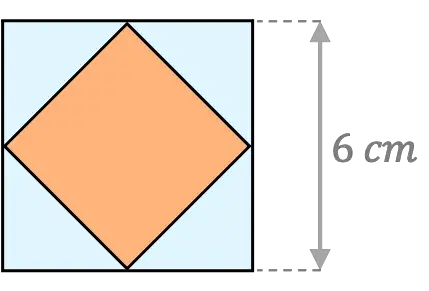
Tal y como se ve en el dibujo del cuadrado y el rombo, la longitud de una diagonal del rombo es equivalente a la longitud del lado del cuadrado. Por tanto, una diagonal del rombo mide 6 cm.
Por otra parte, sabemos que todos los lados de un cuadrado son iguales, de modo que la otra diagonal del rombo también mide 6 cm.
Entonces, para determinar el área del rombo dentro del cuadrado solo nos queda usar la fórmula:
Si te fijas bien, se puede deducir que el área de un rombo dentro de un cuadrado es la mitad del área de dicho cuadrado.
Ejercicio 3
Si el perímetro de un rombo es 20 cm y su diagonal mayor mide 8 cm, calcula el área de dicho rombo.
Gracias a las características geométricas del rombo, sabemos que todos los lados de un rombo son iguales. De manera que podemos calcular cuánto mide uno de sus lados dividiendo su perímetro entre cuatro:
En segundo lugar, dividimos entre dos la longitud de la diagonal mayor para encontrar el otro lado del triángulo inscrito en el rombo:
De manera que dentro del rombo tenemos cuatro triángulos iguales inscritos con las siguientes dimensiones:
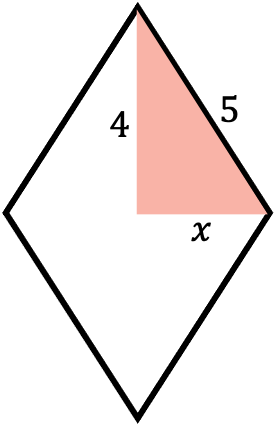
Y como el triángulo de dentro del rombo es rectángulo, podemos utilizar el teorema de Pitágoras para encontrar el valor de la incógnita x:
Así que la diagonal menor del rombo será:
Finalmente, una vez hemos calculado el valor de la otra diagonal del rombo, podemos hallar su área aplicando la fórmula:

