▷ Cuadrado

En este post te explicamos qué son los cuadrados y cuáles son sus características. También te enseñamos cómo calcular la diagonal, el perímetro y el área de un cuadrado. Además, encontrarás una calculadora online con la que podrás calcular las propiedades geométricas de cualquier cuadrado.

Índice

¿Qué es un cuadrado?

El cuadrado es una figura geométrica plana que tiene cuatro lados iguales paralelos dos a dos y cuatro ángulos internos rectos (90º).

👉 Más abajo encontrarás una calculadora para calcular el área y el perímetro de cualquier cuadrado.

Por lo tanto, el cuadrado es un cuadrilátero, porque tiene cuatro lados, y un paralelogramo, pues los lados opuestos son iguales y paralelos dos a dos. Además, los cuadrados se clasifican como polígonos regulares porque todos sus lados y todos sus ángulos son iguales.

Asimismo, el cuadrado cumple con la definición de rectángulo, ya que también se puede definir como un rectángulo con dos lados adyacentes iguales.

➤ Ver: Rectángulo

Características de un cuadrado

Las características del cuadrado son:

Lados de un cuadrado: tiene cuatro lados iguales.
Vértices de un cuadrado: tiene cuatro vértices.
Ángulos de un cuadrado: tiene cuatro ángulos rectos (90º).
Diagonales de un cuadrado: tiene dos diagonales iguales perpendiculares entre sí, las cuales son las bisectrices de los ángulos interiores.
Centro de un cuadrado: el punto donde se cruzan las dos diagonales.
Ejes de simetría de un cuadrado: tiene cuatro ejes de simetría; sus diagonales y las dos líneas imaginarias perpendiculares a los lados que pasan por el centro de la figura.

Ten en cuenta que el cuadrado es una figura geométrica muy parecida al rombo, de hecho, estos dos tipos de paralelogramos se suelen confundir. Puedes ver cuáles son las diferencias entre un cuadrado y un rombo en el siguiente enlace:

➤ Ver: Rombo

Diagonal de un cuadrado

La diagonal de un cuadrado es el segmento que une dos vértices no consecutivos, por lo tanto, un cuadrado tiene dos diagonales.

Para calcular cuánto mide la diagonal de un cuadrado se debe multiplicar la longitud de su lado por la raíz de dos. Así que la fórmula para calcular la diagonal de un cuadrado es la siguiente:

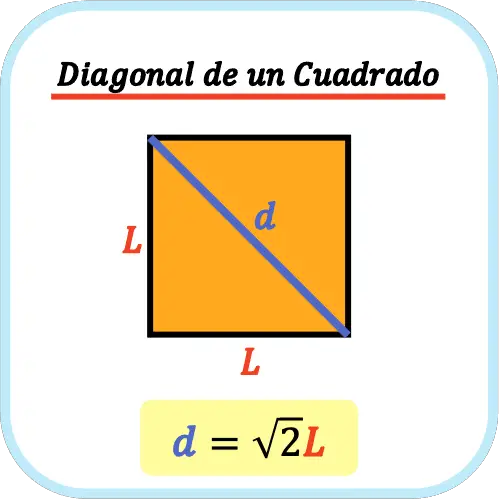
Puedes ver la demostración de la fórmula aquí:

➤ Ver: Diagonal de un cuadrado

Perímetro de un cuadrado

El perímetro de un cuadrado es la suma de sus cuatro lados iguales, por lo tanto, el perímetro de un cuadrado es igual a cuatro por la longitud de uno de sus lados.

Así pues, la fórmula para calcular el perímetro de un cuadrado es la siguiente:

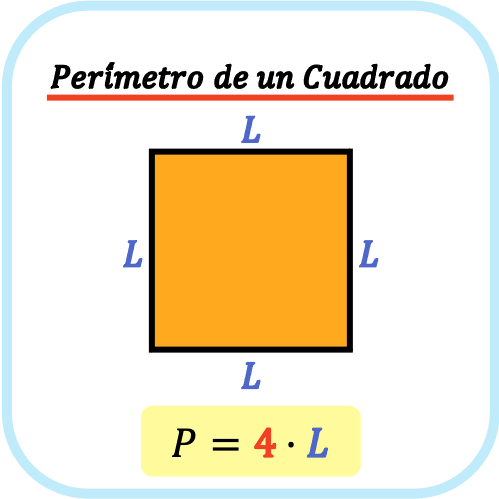
Sin embargo, hay veces que no sabemos la longitud del lado del cuadrado, sino que solo conocemos su diagonal. En estos casos, tenemos que utilizar la siguiente fórmula para calcular el perímetro de un cuadrado a partir de su diagonal:

$P=\cfrac{4\cdot D}{\sqrt{2}}$

➤ Ver: Perímetro de un cuadrado

Área de un cuadrado

El área de un cuadrado es igual a su base por su altura. Por lo tanto, como todos los lados de un cuadrado son iguales, el área de un cuadrado es igual a la longitud de su lado elevada al cuadrado.

Entonces, la fórmula para calcular el área de un cuadrado es la siguiente:

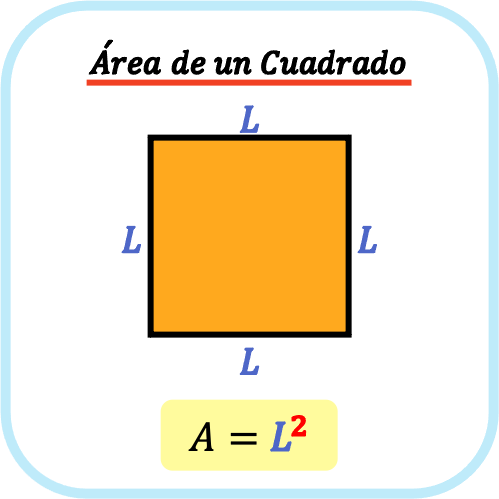
La fórmula anterior es idónea si se conoce la longitud del lado del cuadrado. Sin embargo, si solo sabemos cuánto mide la diagonal del cuadrado y no su lado, debemos usar la siguiente fórmula en la que solo aparece su diagonal:

$A=\cfrac{D^2}{2}$

➤ Ver: Área de un cuadrado

Ejercicio resuelto de un cuadrado

Después de ver cuáles son las fórmulas del cuadrado, te dejamos un ejercicio resuelto de este tipo de cuadriláteros para que puedas ver cómo se calcula la diagonal, el perímetro y el área de un cuadrado.

Calcula la diagonal, el perímetro y el área de un cuadrado cuyo lado mide 6 cm.

Para calcular la diagonal del cuadrado tenemos que multiplicar la longitud de su lado por la raíz cuadrada de dos:

$\begin{aligned}d&=\sqrt{2}\cdot L\\[2ex]d&=\sqrt{2}\cdot 6\\[2ex]d&=8,49 \text{ cm}\end{aligned}$

En segundo lugar, para hallar el perímetro del cuadrado basta con multiplicar el lado del cuadrado por cuatro, ya que el cuadrado tiene cuatro lados y todos son iguales.

$\begin{aligned}P&=4\cdot L\\[2ex]P&=4\cdot 6\\[2ex]P&=24 \text{ cm}\end{aligned}$

Finalmente, el área del cuadrado se calcula elevando la longitud de su lado a la dos:

$\begin{aligned}A&= L^2\\[2ex]A&=6^2\\[2ex]A&=36 \text{ cm}^2\end{aligned}$

Calculadora del cuadrado

Introduce la longitud del lado o de la diagonal en la siguiente calculadora y luego pulsa el botón de abajo para calcular el área y el perímetro del cuadrado.