Área de un prisma triangular: fórmula, ejemplo y calculadora

En este post se explica cómo calcular el área de un prisma triangular. También encontrarás ejercicios resueltos de áreas de prismas triangulares y, además, una calculadora online para calcular el área de un prisma regular.

Sin embargo, la fórmula para calcular el área de un prisma triangular depende de si es un prisma regular o irregular, de modo que veremos los dos casos posibles. Recuerda que un prisma triangular regular es aquel cuya base es un triángulo equilátero, por otra parte, un prisma triangular no regular significa que las longitudes de los lados de la base son diferentes.

Índice

Área de un prisma triangular regular

El área de un prisma triangular regular es igual a la longitud del lado del triángulo de la base multiplicado por la suma del triple de la altura del prisma más la raíz de tres por el lado partido por dos.

Es decir, la fórmula para calcular el área de un prisma triangular regular es la siguiente:

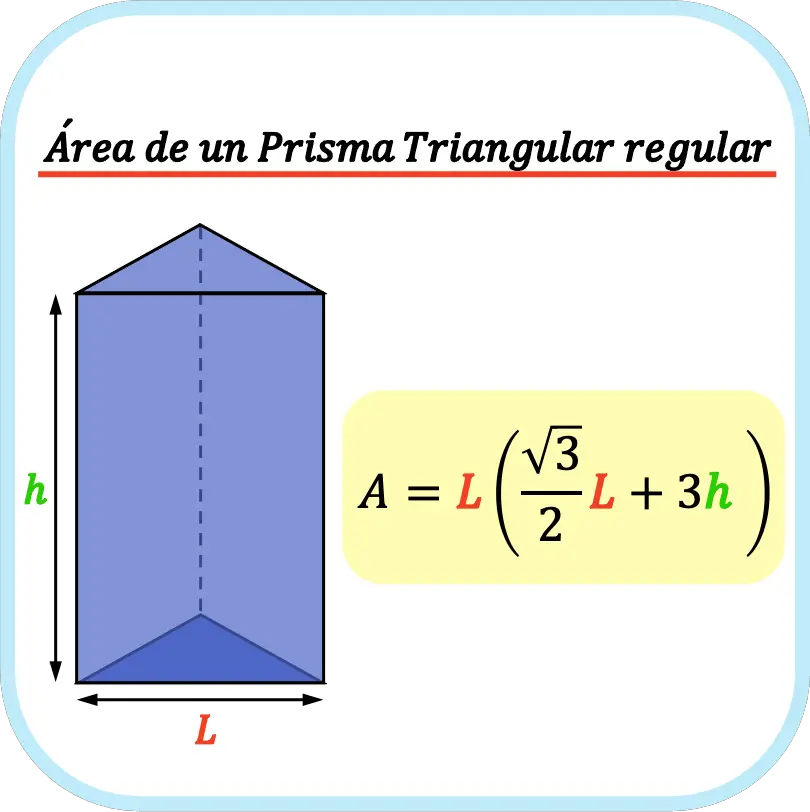
formula del area de un prisma triangular regular

👉 Puedes utilizar la calculadora que hay más abajo para calcular el área de cualquier prisma triangular regular.

Ver demostración de la fórmula

El área total de cualquier tipo de prisma regular se calcula sumando las áreas de las dos bases más el área lateral del prisma:

$A=2\cdot A_b+A_{lateral}$

Las bases de un prisma triangular regular son triángulos equiláteros y las caras laterales son rectángulos. Por lo tanto, sustituimos la fórmula del área de un triángulo equilátero y la fórmula del área de un rectángulo en la expresión anterior:

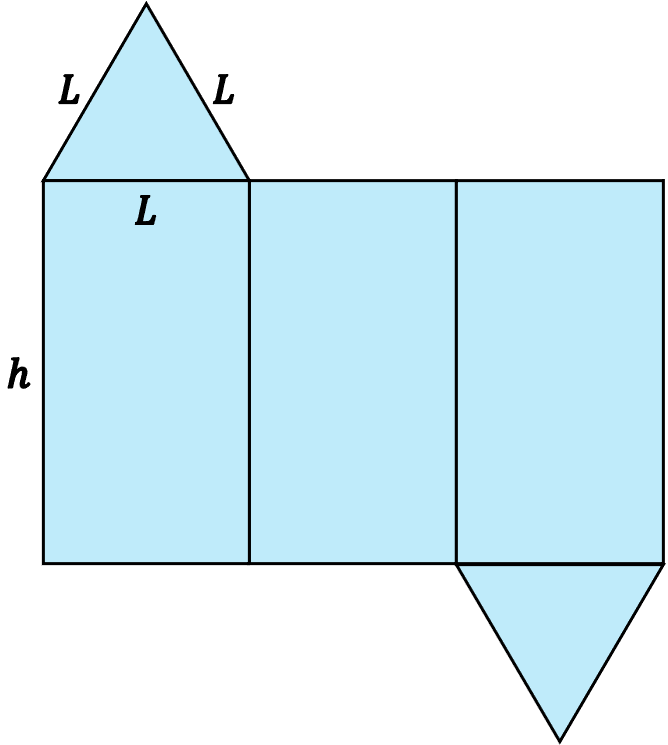
despliegue de un prisma triangular regular

$A=2\cdot \cfrac{\sqrt{3}}{4}\cdot L^2+3\cdot L\cdot h$

Finalmente, simplificamos la expresión para obtener la fórmula de la superficie de un prisma triangular regular:

$A=\cfrac{\sqrt{3}}{2}\cdot L^2+3\cdot L\cdot h$

$\displaystyle A=L\cdot \left(\frac{\sqrt{3}}{2}\cdot L+3\cdot h\right)$

Ejemplo del cálculo del área de un prisma triangular regular

Una vez hemos visto cuál es la fórmula del área de un prisma triangular regular, vamos a ver cómo se calcula mediante un ejemplo resuelto.

Calcula el área del siguiente prisma triangular recto:

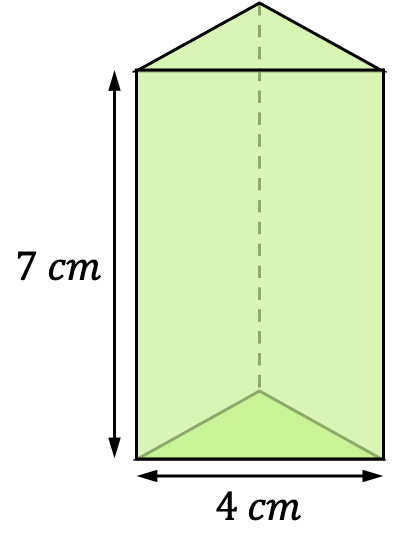
ejemplo del area de un prisma triangular regular

Para sacar el área del prisma triangular regular, debemos usar la fórmula que hemos visto más arriba:

$\displaystyle A=L\cdot \left(\frac{\sqrt{3}}{2}\cdot L+3\cdot h\right)$

De modo que sustituimos los datos en la fórmula y hacemos el cálculo de la superficie total del prisma triangular:

$\displaystyle A=4\cdot \left(\frac{\sqrt{3}}{2}\cdot 4+3\cdot 7\right)=97,86\text{ cm}^2$

Calculadora del área y volumen de un prisma triangular regular

Introduce la longitud del lado de la base y de la altura del prisma triangular regular, luego pulsa el botón «Calcular» para calcular el área y el volumen del cuerpo geométrico.

La letra $L$ se refiere al lado de la base triangular, mientras que la letra $h$ representa su altura. Debes introducir los números en centímetros utilizando el punto como separador decimal.

Área de un prisma triangular irregular

Cuando el prisma triangular es irregular, es decir, cuando el triángulo de la base del prisma no es equilátero, no hay una fórmula concreta para calcular su área.

Por lo tanto, para calcular el área de un prisma triangular irregular se debe encontrar el área de las bases del prisma y de sus caras laterales y luego sumarlas.

$A=2\cdot A_{base}+A_{lateral}$

Teniendo en cuenta que la superficie lateral es la suma del área de tres rectángulos:

$A_{lateral}=h\cdot (a+b+c)$

Por otro lado, el área de cualquier triángulo irregular se puede averiguar mediante la fórmula de Herón:

$A_{base}=\sqrt{s(s-a)(s-b)(s-c)}$

Asimismo, recuerda que el semiperímetro es la semisuma de todos los lados del triángulo:

$s=\cfrac{a+b+c}{2}$

Ejemplo del cálculo del área de un prisma triangular irregular

Para que puedas ver cómo se halla el área de un prisma triangular irregular, a continuación tienes un ejercicio resuelto del área de este tipo de cuerpo geométrico.

Halla el área del siguiente prisma triangular no regular:

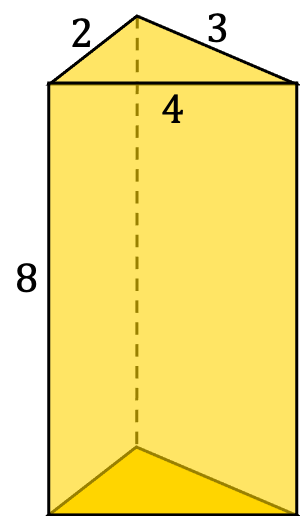
La superficie de un prisma triangular irregular es equivalente al área de las bases más el área lateral de la figura.

$A=2\cdot A_{base}+A_{lateral}$

De modo que primero calculamos el área de la base del prisma aplicando la fórmula de Herón:

$s=\cfrac{2+3+4}{2}=4,5 \text{ cm}$

$\begin{aligned}A_{base}&=\sqrt{s(s-a)(s-b)(s-c)}\\[2ex] &=\sqrt{4,5\cdot (4,5-2)\cdot (4,5-3)\cdot (4,5-4)}\\[2ex]&=2,90 \text{ cm}^2\end{aligned}$

En segundo lugar, hallamos el área lateral del cuerpo geométrico:

$\begin{aligned}A_{lateral}&=h\cdot (a+b+c)\\[2ex]&= 8\cdot (2+3+4) \\[2ex] &=72 \text{ cm}^2\end{aligned}$

Por último, sumamos las dos áreas calculadas para obtener el área total del prisma triangular irregular:

$\begin{aligned}A&=2\cdot A_{base}+A_{lateral}\\[2ex]&=2 \cdot 2,90 + 72\\[2ex]&=77,80\text{ cm}^2\end{aligned}$

Calculadora del área y volumen de un prisma triangular irregular

Introduce las longitudes de los lados de la base y de la altura del prisma triangular irregular, luego pulsa el botón «Calcular» para calcular el área y el volumen del cuerpo geométrico. Debes introducir los números en centímetros utilizando el punto como separador decimal.