Aquí encontrarás cómo se calcula el perímetro de un sector circular. Además, calculamos el perímetro de un sector circular a modo de ejemplo.
Índice
Cómo calcular el perímetro de un sector circular
El perímetro de un sector circular es igual a la suma de los lados del sector circular (que son los radios del círculo) más la longitud del arco del sector circular.
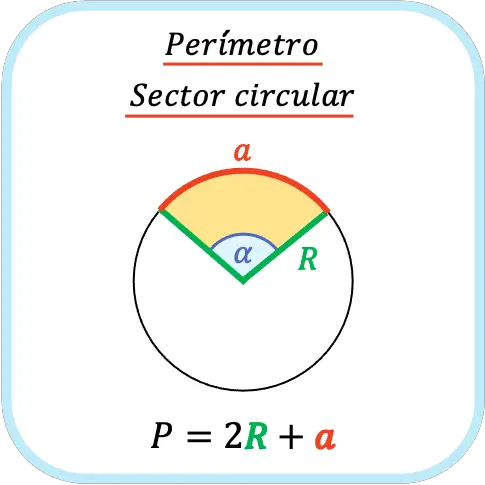
Como puedes comprobar, hallar el perímetro de un sector circular no es complicado, porque simplemente debes hacer una multiplicación y una suma. Sin embargo, el problema surge cuando no nos dan la longitud del arco del sector circular, que es la mayoría de las veces, ya que entonces debemos hacer un cálculo previo.
Así pues, la longitud del arco de un sector circular se calcula utilizando la fórmula del perímetro de un círculo, ya que en realidad el arco es la parte proporcional al ángulo del sector circular de todo el perímetro del círculo.
Por tanto, la fórmula para calcular el sector circular también se puede expresar de la siguiente manera:
Ten en cuenta que esta fórmula solamente se puede aplicar si el ángulo está expresado en grados, pero si el ángulo está en forma de radianes debes usar la siguiente fórmula para hallar el perímetro de un sector circular:
Ejemplo del perímetro de un sector circular
Vista cuál es la fórmula del perímetro de un sector circular, a continuación vamos a explicar un ejemplo para que entiendas del todo cómo se saca el perímetro de un sector circular.
- Calcula el perímetro del siguiente sector circular de ángulo 100º que está inscrito en un círculo de 8 cm de radio.
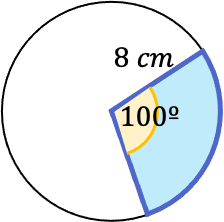
Como hemos visto antes, para encontrar el perímetro del sector circular debemos sumar la longitud de sus lados y de su arco.
El valor del radio ya lo conocemos, por lo que primero tenemos que determinar la longitud del arco empleando su fórmula correspondiente:
Y, finalmente, sustituimos los valres del radio y del arco en la fórmula del sector circular y hacemos el cálculo:

