En este post te explicamos cómo hallar el área de un sector circular. Además, podrás practicar con ejercicios resueltos del área de un sector circular. Y, finalmente, podrás ver la fórmula del área del sector circular.
Índice
Cómo calcular el área de un sector circular
El área de un sector circular es igual al número pi por el radio del sector circular al cuadrado por el ángulo del sector circular (en grados) dividido por 360.
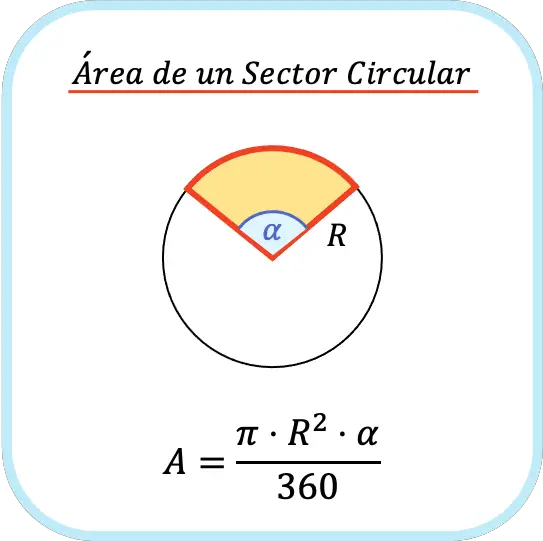
Ten en cuenta que esta fórmula solo puede utilizarse si el ángulo está en grados. Cuando el ángulo está expresado en radianes tienes dos opciones para hacer el cálculo del área de un sector circular: pasar el ángulo a grados y aplicar la fórmula anterior, o usar directamente la siguiente fórmula:
Por otro lado, también se puede hallar el área de un sector circular sin saber su ángulo si se conoce su radio y la longitud del arco del sector circular:
Ejemplo del área de un sector circular
Una vez hemos vista cuál es la fórmula del área de un sector, a continuación vamos a hallar el área de una figura geométrica de este tipo. Así te resultará más fácil entender cómo se calcula el área de un sector circular.
- Halla el área de un sector circular de 7 cm de radio y ángulo 80º.
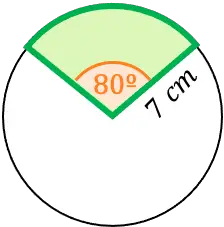
Como hemos visto más arriba, la fórmula para calcular el área de un sector circular es la siguiente:
En este caso ya conocemos el radio y el ángulo del sector circular, por lo que para encontrar su área simplemente tenemos que sustituir los datos en la fórmula:
Y hacer todos los cálculos:
Demostración de la fórmula del área de un sector circular
En este apartado vamos a demostrar la fórmula del área del sector circular. Evidentemente, no es necesario que te aprendas de memoria la demostración, pero siempre ayuda a entender mejor los conceptos saber de dónde vienen las fórmulas.
Para demostrar la fórmula del área de un sector circular partiremos de la fórmula del área de un círculo:
En realidad, un círculo es un sector circular de 360º, por lo tanto, para calcular el área de un sector circular de un determinado ángulo simplemente tenemos que multiplicar la expresión algebraica anterior por la proporción de ángulo que ocupa dicho sector circular:
De manera que podemos llegar a la fórmula del área de un sector circular solamente utilizando la lógica, ya que en realidad se trata de una fórmula proporcional al área de un círculo entero.
Ejercicios resueltos del área de un sector circular
Ejercicio 1
Calcula el área del siguiente sector circular:
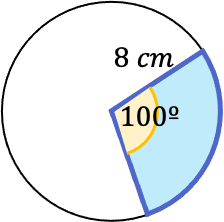
Para determinar el área aplicamos la fórmula del sector circular:
Y sustituimos los valores en la fórmula y resolvemos los cálculos:
Ejercicio 2
Encuentra el área del siguiente sector circular sin ángulo inscrito en un cuadrado:
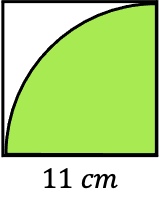
Aunque no se especifique el ángulo del sector circular, como el sector circular está dentro de un cuadrado y toca sus dos vértices opuestos, significa que el sector ocupa un cuarto de un círculo entero. Por lo tanto, el ángulo del sector circular es 90 grados.
Entonces, solamente nos queda usar la fórmula correspondiente:
Y finalmente hallamos el área del sector circular del problema:

