En este post te explicamos cómo calcular el área de una corona circular. Encontrarás ejercicios resueltos del área de una corona circular, e incluso podrás calcular el área y el perímetro de cualquier corona circular con la calculadora online que hay al final.
Índice
Fórmula del área de una corona circular
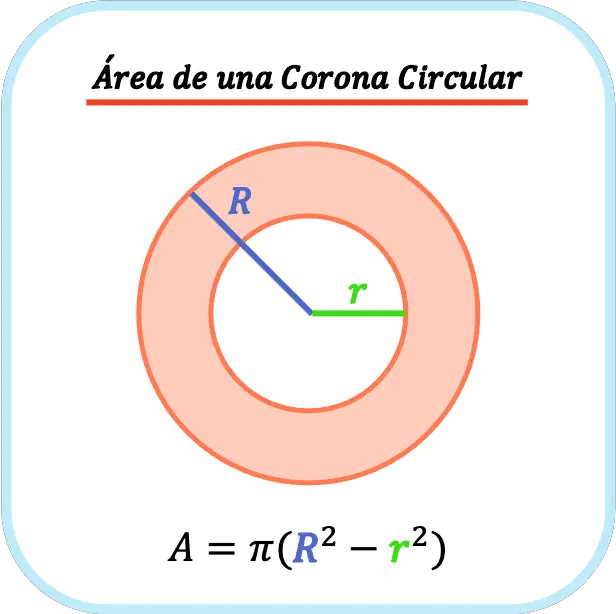
El área de una corona circular es el área del círculo mayor menos el área del círculo menor. Por lo tanto, el área de una corona circular es igual a pi por la diferencia de los cuadrados de los radios de la corona circular.
En definitiva, la fórmula para calcular el área de una corona circular es la siguiente:
👉 Puedes utilizar la calculadora que hay más abajo para calcular el área de cualquier corona circular.
En definitiva, para calcular el área de una corona circular tienes que elevar al cuadrado el radio exterior y el radio interior de la corona circular, restarlos y multiplicar el resultado por el número pi.
Ejemplo del área de una corona circular
Ahora que ya sabemos cuál es la fórmula del área de una corona circular, vamos a calcular el área de una figura circular de este tipo a modo de ejemplo.
- Calcula el área sombreada de la siguiente corona circular cuyo radio exterior mide 10 cm y su radio interior 5 cm.
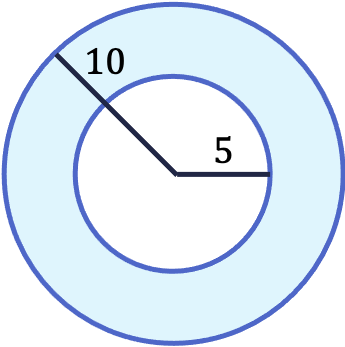
Para calcular la superficie de la corona circular simplemente debemos utilizar su fórmula:
Ahora sustituimos el valor del radio exterior y del radio interior en la fórmula y hacemos el cálculo del área de la corona circular:
![\begin{aligned}A& =\pi \cdot(10^2-5^2)\\[2ex]&=\pi \cdot (100-25)\\[2ex]&=\pi \cdot 75 \\[2ex]&=235,62 \text{ cm}^2\end{aligned}](https://www.areasyvolumenes.net/wp-content/ql-cache/quicklatex.com-6514185adde72c7f7164417f26d85d47_l3.svg "Rendered by QuickLaTeX.com")
Calculadora del área y perímetro de una corona circular
Introduce la longitud del radio exterior y del radio interior en la siguiente calculadora para calcular el área y el perímetro de la corona circular de manera online.
Debes introducir los números en centímetros utilizando el punto como separador decimal.
Ejercicios resueltos del área de una corona circular
Ejercicio 1
¿Cuál es el área total de la corona circular cuyos radios miden 7 cm y 4 cm?
Para sacar el área de la corona circular aplicamos su fórmula:
Y sustituimos los datos del enunciado del problema en la fórmula y calculamos el área de la corona circular:
![\begin{aligned}A& =\pi \cdot(7^2-4^2)\\[2ex]&=\pi \cdot (49-16)\\[2ex]&=\pi \cdot 33 \\[2ex]&=103,67 \text{ cm}^2\end{aligned}](https://www.areasyvolumenes.net/wp-content/ql-cache/quicklatex.com-1321a63ef225ec069805297ccf2b3a8f_l3.svg "Rendered by QuickLaTeX.com")
Ejercicio 2
De una corona circular solo sabemos que tiene una cuerda tangente a la circunferencia más pequeña de longitud 6 cm. A partir de este dato, encuentra el área de la corona circular.
Para determinar el área de la corona circular, tenemos que averiguar la diferencia entre los cuadrados de los radios de la figura plana. Pero en este ejercicio no nos dan ninguna información al respecto.
Sin embargo, podemos relacionar la longitud de la cuerda de la corona circular con sus radios utilizando el teorema de Pitágoras:
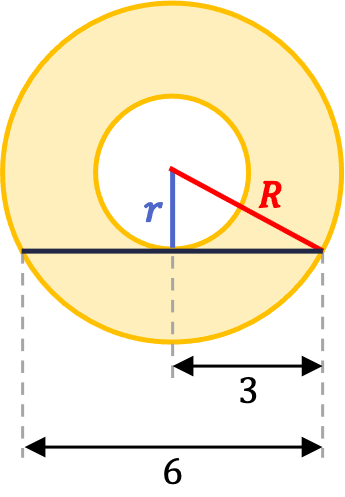
Entonces, ahora que conocemos la relación entre los cuadrados de los radios, podemos calcular fácilmente el área de la corona circular usando la fórmula:
![\begin{aligned}A& =\pi\cdot (R^2-r^2)\\[2ex] &=\pi \cdot 9\\[2ex]&=28,27 \text{ cm}^2\end{aligned}](https://www.areasyvolumenes.net/wp-content/ql-cache/quicklatex.com-2ebd6ef8c2e947ad27c065422aa3efb5_l3.svg "Rendered by QuickLaTeX.com")
Ejercicio 3
Calcula la superficie sombreada de la siguiente corona circular:
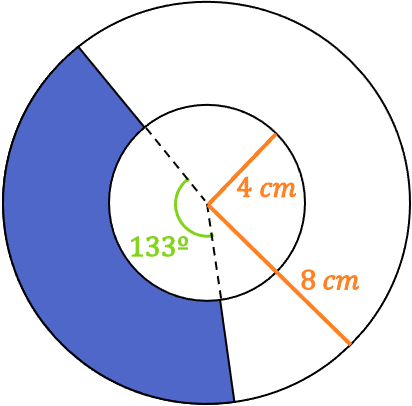
La figura circular representada en este ejercicio se llama trapecio circular, y se trata de una parte de una corona circular. Por lo tanto, para encontrar el área de la zona sombreada debemos emplear la fórmula de la corona circular y multiplicarla por la parte proporcional del ángulo del trapecio circular:
Ahora sustituimos los valores del trapecio circular en la fórmula y calculamos su área:
