En este post te explicamos cómo calcular el área de un círculo. Podrás ver ejemplos resueltos del área de un círculo y, además, calcular el área y el perímetro de cualquier círculo con la calculadora online que encontrarás al final.
Índice
¿Qué es el área de un círculo?
Antes de ver cuál es la fórmula del área de este tipo de figura geométrica, vamos a definir rápidamente qué es el área de un círculo para entender mejor el concepto.
El área de un círculo es el número de unidades cuadradas que hay dentro de un círculo. Si lo explicásemos para niños, podríamos decir que el área de un círculo es el número de cuadrados diminutos que caben dentro del círculo.
Hay que tener en cuenta la diferencia entre círculo y circunferencia, pues la circunferencia es la línea exterior que rodea el círculo, pero el círculo es toda la superficie del interior de la circunferencia. Por lo que es incorrecto calcular el área de una circunferencia, sino que calculamos el área de un círculo.
Fórmula del área de un círculo
El área de un círculo es igual al número pi por el radio del círculo al cuadrado. Por lo tanto, para calcular el área de un círculo debemos elevar su radio al cuadrado y luego multiplicarlo por la longitud del radio del círculo.
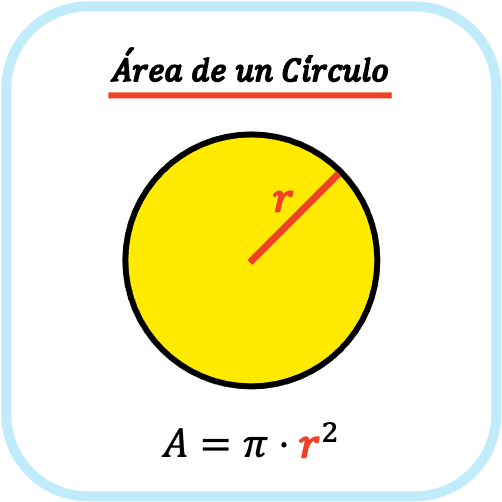
👉 Puedes utilizar la calculadora que hay más abajo para calcular el área de cualquier círculo.
Como ya sabes, el radio de un círculo es la mitad de su diámetro. Por tanto, podemos modificar la expresión anterior para tener una fórmula para calcular el área de un círculo sabiendo el diámetro:
Entonces, para calcular el área de un círculo con su diámetro primero tenemos que elevar el diámetro al cuadrado, luego multiplicarlo por el número pi, y finalmente dividir entre 4.
Ejemplo del área de un círculo
En este apartado veremos cómo sacar el área de un círculo resolviendo un ejemplo paso a paso.
- ¿Cuál es el área de un círculo cuyo radio mide 5 cm?
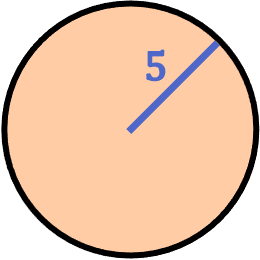
En este caso conocemos el valor del radio de la figura circular, así que debemos utilizar la fórmula de la superficie de un círculo con el radio:
Ahora sustituimos el valor del radio en la fórmula y hacemos el cálculo del área del círculo:
Calculadora del área y perímetro de un círculo
Introduce la longitud del radio o del diámetro en la siguiente calculadora para calcular el área y el perímetro de un círculo de manera online.
Debes seleccionar si pondrás el radio o el diámetro del círculo e introducir el número en centímetros utilizando el punto como separador decimal.
Ejercicios resueltos del área de un círculo
Ejercicio 1
Calcula el área del siguiente círculo cuyo diámetro mide 13 cm.
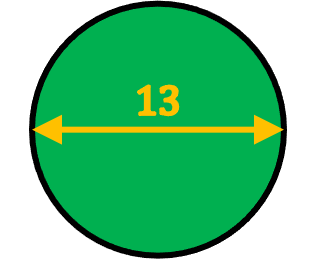
En este ejercicio no sabemos cuánto mide el radio, sino que nos dan la longitud del diámetro del círculo. De modo que podemos utilizar directamente la fórmula de la superficie de un círculo con el diámetro:
Sustituimos el valor del diámetro en la fórmula y calculamos el área del círculo:
Ejercicio 2
Sabemos que el área de un círculo es de 50 cm2. Si se triplica la longitud del radio de ese círculo, ¿cuánto es el área del nuevo círculo?
En la fórmula del área de este tipo de figura circular aparece el radio, de modo que el área de un círculo depende de la longitud de su radio. Y, en consecuencia, si aumentamos su radio su área también habrá aumentado.
Entonces, ponemos en la fórmula el radio multiplicado por 3 para averiguar cómo varia el área:
Así pues, al triplicar el valor del radio del círculo su área habrá aumentado 9 veces:
Ejercicio 3
Determina el área del círculo cuyo perímetro mide 100,53 cm.
En primer lugar, tenemos que encontrar la longitud del radio del círculo despejando de la fórmula del perímetro de un círculo:
Y una vez ya sabemos el radio de la figura, simplemente tenemos que aplicar la regla del área de un círculo:
Ejercicio 4
Calcula el área del siguiente círculo inscrito en un cuadrado de 7 cm de lado.
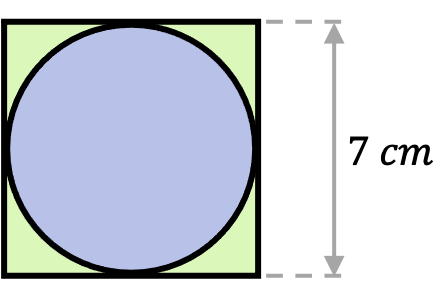
Para resolver este problema basta con deducir que el lado del cuadrado mide exactamente lo mismo que el diámetro del círculo. De manera que el diámetro de la figura circular es de 7 cm.
Y ahora tan solo tenemos que aplicar la fórmula del área de un círculo con el diámetro para hallar la superficie del círculo de dentro del cuadrado:

