En este post se explica cómo calcular el volumen de un prisma pentagonal. Además, encontrarás un ejercicio resuelto del cálculo del volumen de un prisma pentagonal y una calculadora online para hallar el volumen de cualquier prisma pentagonal regular.
Índice
Fórmula del volumen de un prisma pentagonal
El volumen de un prisma pentagonal se calcula multiplicando el área del pentágono de la base por la altura del prisma. Por lo tanto, el volumen de un prisma pentagonal regular es igual a la altura del prisma pentagonal por cinco por el lado del pentágono por su apotema dividido entre dos.
En definitiva, la fórmula para calcular el volumen de un prisma pentagonal regular es la siguiente:
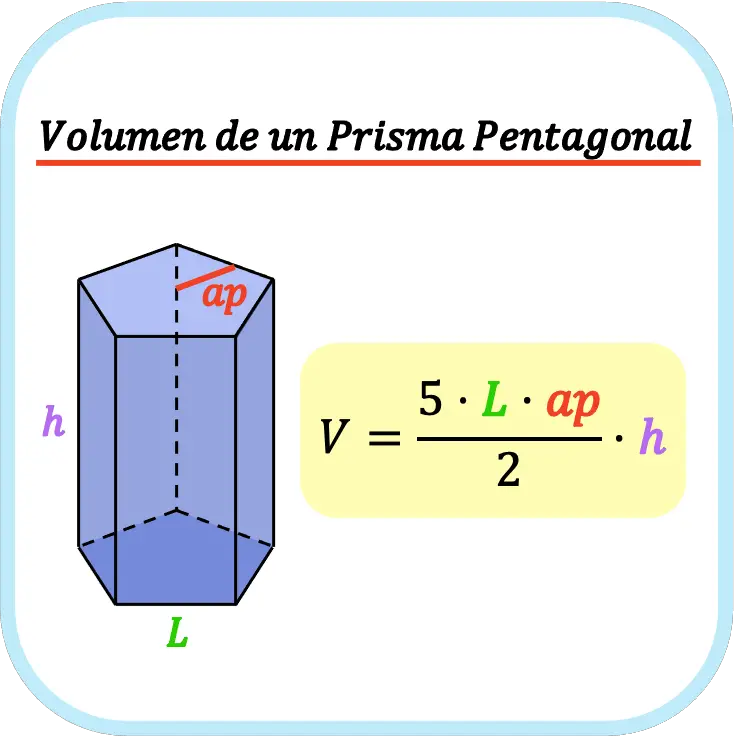
👉 Puedes usar la calculadora que hay más abajo para calcular el volumen de cualquier prisma pentagonal regular.
Ten presente que esta fórmula solo se puede utilizar si el prisma pentagonal es regular. Por si lo necesitas, más abajo se explica cómo sacar el área de un prisma pentagonal irregular.
Es muy sencillo obtener la fórmula del volumen de un prisma regular con cinco caras laterales. El cálculo del volumen de un prisma se hace multiplicando el área de la base por su altura, así pues, basta con sustituir la fórmula del área del pentágono regular para encontrar la fórmula del volumen de un prisma pentagonal regular:
![\begin{aligned}V&=A_{base}\cdot h\\[2ex]V&=\cfrac{5\cdot L\cdot ap}{2}\cdot h\end{aligned}](https://www.areasyvolumenes.net/wp-content/ql-cache/quicklatex.com-ce1d898b8d10b01bf8edc4ae040a32f3_l3.svg "Rendered by QuickLaTeX.com")
Además, la apotema de un polígono regular y la longitud de su lado se pueden relacionar matemáticamente utilizando trigonometría:
En consecuencia, también podemos obtener una fórmula del volumen de un pentágono regular solo con el lado y la altura. Para ello, basta con sustituir la expresión anterior en la fórmula de arriba:
![\begin{aligned}\displaystyle V&=\frac{5\cdot L\cdot ap}{2}\cdot h\\[2ex]\displaystyle V&=\frac{5\cdot L\cdot L}{2\cdot 1,45}\cdot h\\[2ex]\displaystyle V&=\frac{5\cdot L^2}{2,90}\cdot h\\[2ex]\displaystyle V&=1,72\cdot L^2\cdot h\end{aligned}](https://www.areasyvolumenes.net/wp-content/ql-cache/quicklatex.com-b5abee167c57ef035a10358b623b1af3_l3.svg "Rendered by QuickLaTeX.com")
Ejemplo del volumen de un prisma pentagonal
Para que puedas ver cómo se calcula el volumen de un prisma pentagonal, a continuación tienes un ejemplo resuelto de este tipo de prismas.
- Halla el volumen del siguiente prisma pentagonal regular:
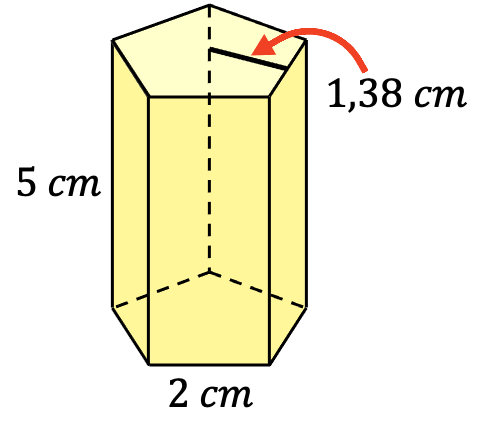
En este problema ya sabemos cuánto mide el lado del pentágono, su apotema y la altura del prisma pentagonal. Así que solamente tenemos que aplicar su fórmula correspondiente:
Entonces, sustituimos los valores en la fórmula y calculamos el volumen del prisma pentagonal regular:
Calculadora del área y volumen de un prisma pentagonal
Introduce el lado o la apotema del pentágono y la altura del prisma pentagonal, luego pulsa el botón «Calcular» para calcular el área y el volumen del cuerpo geométrico. Debes introducir los números en centímetros utilizando el punto como separador decimal.
Volumen de un prisma pentagonal irregular
Si el prisma pentagonal es irregular, lo que significa que los lados de la base son diferentes, es decir, los pentágonos de las bases son irregulares, no podemos utilizar la fórmula vista arriba porque un polígono irregular no tiene apotema.
Entonces, para calcular el volumen de un prisma pentagonal irregular primero tenemos que hallar el área de la base y luego multiplicar por la altura del prisma pentagonal.
En general, la base de prismas irregulares tiene una forma poco habitual, de manera que para encontrar su área normalmente se divide el polígono en diferentes figuras más pequeñas y, posteriormente, se suman todas las áreas calculadas para sacar el área total de la base.
