En este post te explicamos cómo se calcula el perímetro de un heptágono. Podrás ver un ejemplo del cálculo del perímetro de un heptágono y, además, encontrarás una calculadora para calcular el perímetro y el área de cualquier heptágono.
Índice
Fórmula del perímetro de un heptágono
El perímetro de un heptágono es la suma de las longitudes de sus siete lados. Por lo tanto, el perímetro de un heptágono regular es igual a siete por la longitud de uno de sus lados.
De manera que la fórmula del perímetro de un heptágono es la siguiente:
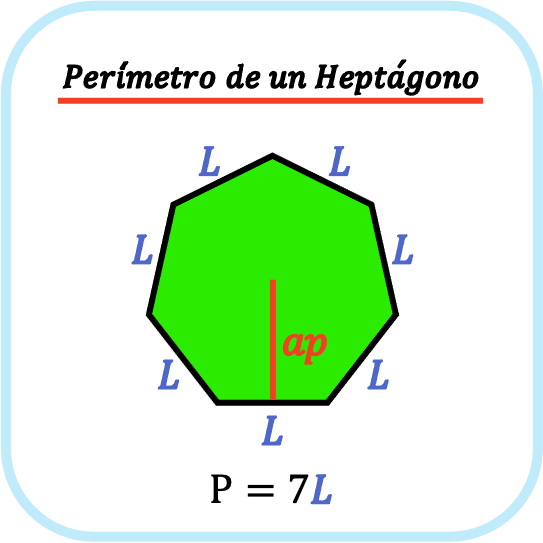
👉 Puedes usar la calculadora que hay más abajo para calcular el perímetro de cualquier heptágono regular.
Lógicamente, solo se puede usar la fórmula del perímetro de un heptágono cuando este es regular, es decir, cuando todos sus lados son iguales. Pero si el heptágono es irregular significa que alguno de sus lados mide diferente y, por lo tanto, tenemos que sumar la longitud de todos los lados de la figura por separado.
Asimismo, no es necesario conocer el valor de la apotema del heptágono para poder hallar su perímetro, sabiendo su lado es suficiente.
Ejemplo del perímetro de un heptágono
Una vez sabemos cuál es la fórmula del perímetro de un heptágono, vamos a resolver un ejercicio de este tipo de figura plana a continuación. La idea es que veas cómo se saca el perímetro de un heptágono.
- Calcula el perímetro de un heptágono regular cuyo lado mide 9 cm.
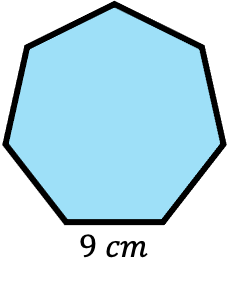
Se trata de un heptágono regular, así que los siete lados del polígono miden lo mismo. Por lo tanto, simplemente debemos aplicar la fórmula del perímetro de un heptágono para encontrar su perímetro:
Y ahora sustituimos en la fórmula el dato de la longitud del lado del heptágono, que es 9 cm, y hacemos el cálculo:
Calculadora del perímetro y área de un heptágono
Introduce la longitud del lado o de la apotema en la siguiente calculadora para calcular el perímetro y el área de un heptágono regular.
Debes seleccionar si pondrás la longitud del lado o de la apotema e introducir el número en centímetros utilizando el punto como separador decimal.
