En este post se explica cómo calcular el área y el perímetro de todas las figuras planas regulares. Así pues, encontrarás las fórmulas de las áreas y los perímetros de las figuras planas.
Índice
Área y perímetro
El perímetro es la longitud del contorno de una figura plana, mientras que el área es la superficie que ocupa una figura plana.
Por lo tanto, la diferencia entre el área y el perímetro es que el área es el espacio que ocupa una figura plana, en cambio, el perímetro es la suma de los lados de una figura plana. De manera que el perímetro de una figura plana delimita su área.
Por ejemplo, si queremos cubrir una mesa con un mantel, tenemos que calcular el área que ocupa la mesa para saber qué tan grande debe ser el mantel. Pero si queremos poner una cinta alrededor de la mesa, debemos hallar el perímetro de la mesa para saber la cantidad de cinta que necesitamos.
Fórmulas de áreas y perímetros de figuras planas
A continuación puedes ver todas las fórmulas de áreas y perímetros de las figuras planas regulares. Así pues, para cada tipo de figura plana podrás ver su fórmula para el área y su fórmula para el perímetro.
Área y perímetro de un triángulo
El área de un triángulo es igual a la base del triángulo por su altura partido por dos. Por lo tanto, para calcular el área de un triángulo se debe multiplicar su base por su altura y luego dividir entre dos.
De modo que la fórmula para calcular el área de un triángulo es la siguiente:
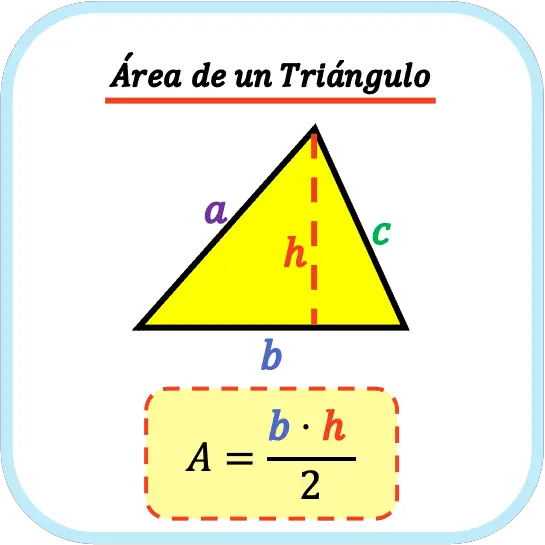
El perímetro de un triángulo es igual a la suma de sus tres lados. Es decir, para calcular el perímetro de un triángulo se deben sumar las longitudes de todos sus lados.
Por lo tanto, la fórmula para calcular el perímetro de un triángulo es la siguiente:
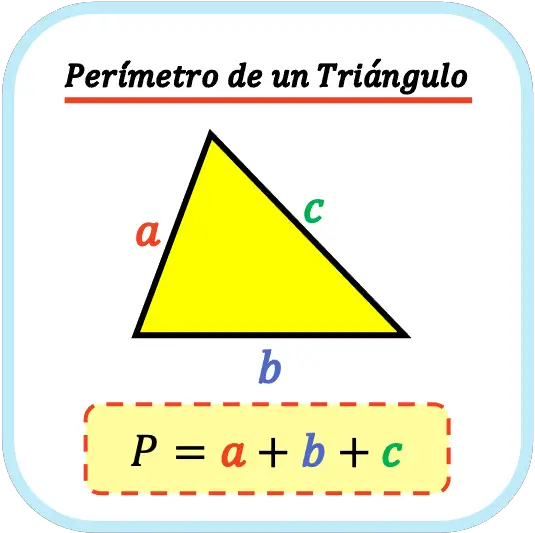
Ten en cuenta que si se trata de un triángulo equilátero, significa que los tres lados del triángulo son idénticos. En tal caso, para hallar el perímetro de este tipo de triángulo basta con multiplicar por tres la longitud de uno de sus lados.
Área y perímetro de un cuadrado
El área de un cuadrado es igual a su base por su altura. Por lo tanto, como todos los lados de un cuadrado son iguales, el área de un cuadrado es igual a la longitud de su lado elevada al cuadrado.
Es decir, la fórmula para calcular el área de un cuadrado es la siguiente:
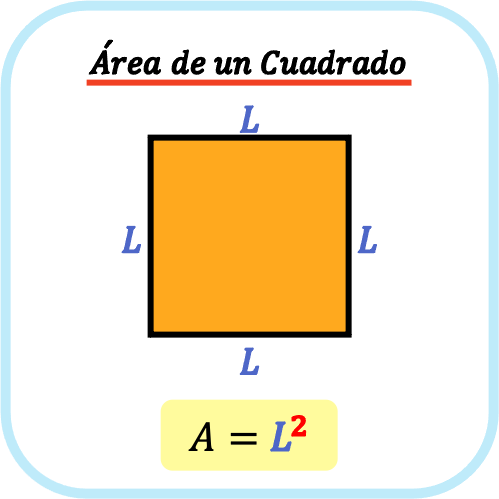
El perímetro de un cuadrado es la suma de sus cuatro lados iguales, por lo tanto, el perímetro de un cuadrado es igual a cuatro por la longitud de uno de sus lados.
Así pues, la fórmula para calcular el perímetro de un cuadrado es la siguiente:
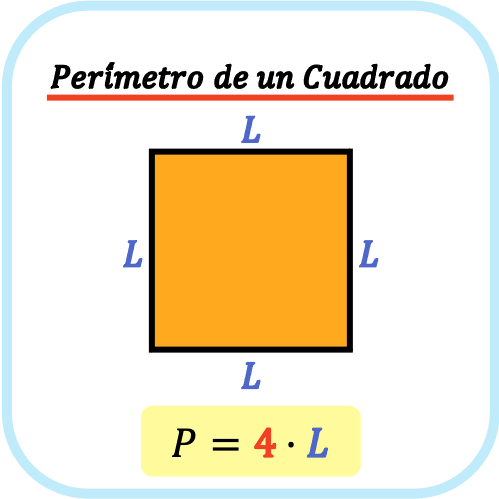
Área y perímetro de un rectángulo
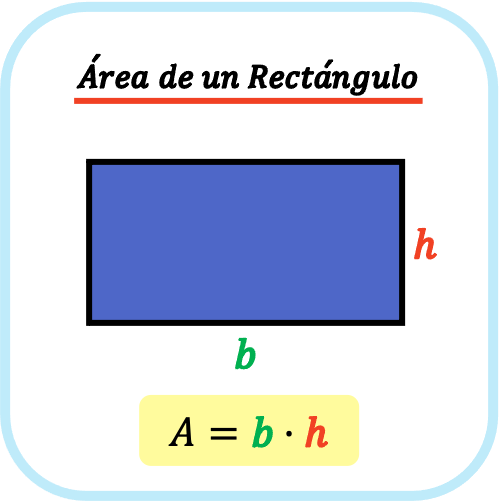
El área de un rectángulo es igual a la base del rectángulo por la altura del rectángulo.
A diferencia del cuadrado, los lados del rectángulo son iguales dos a dos, por lo tanto, tenemos que multiplicar su base por su altura para calcular el área del rectángulo.
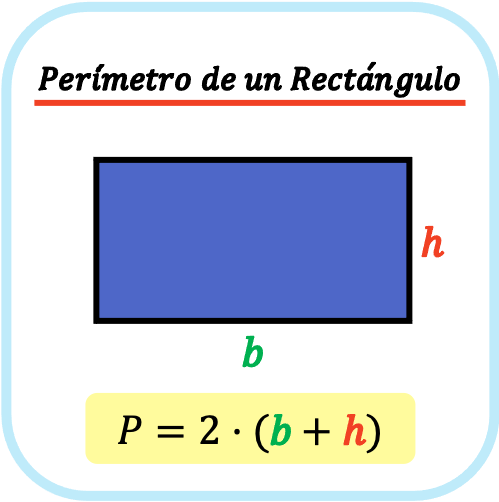
El perímetro de un rectángulo es la suma de sus cuatro lados. Por lo tanto, como un rectángulo tiene los lados iguales dos a dos, el perímetro de un rectángulo es igual a dos por la suma de la base del rectángulo más su altura.
Así que la fórmula para calcular el perímetro de un rectángulo es la siguiente:
Área y perímetro de un rombo
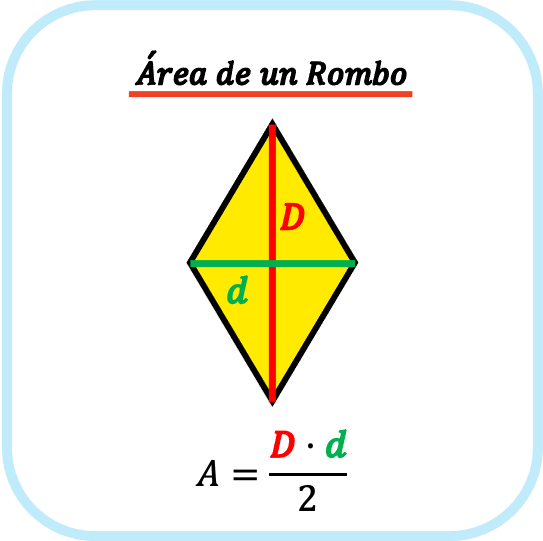
El área de un rombo se calcula a partir de sus diagonales. En concreto, el área de un rombo es igual a la diagonal mayor del rombo por la diagonal menor del rombo partido por dos.
De modo que la fórmula del área de un rombo es:
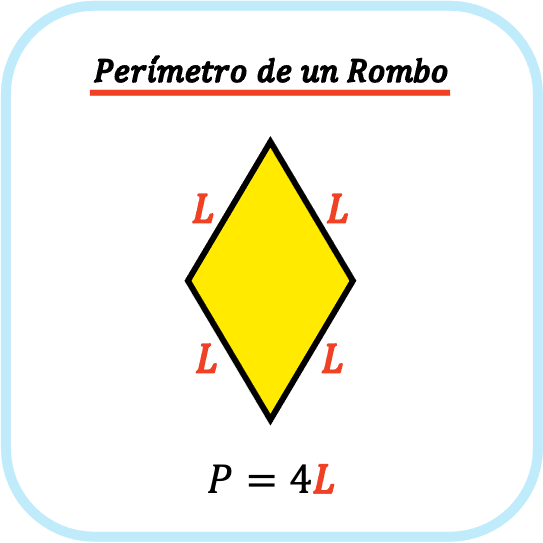
Por otro lado, para hallar el perímetro de un rombo basta con multiplicar por cuatro la longitud de uno de sus lados, ya que sus cuatro lados miden lo mismo.
Área y perímetro de un trapecio
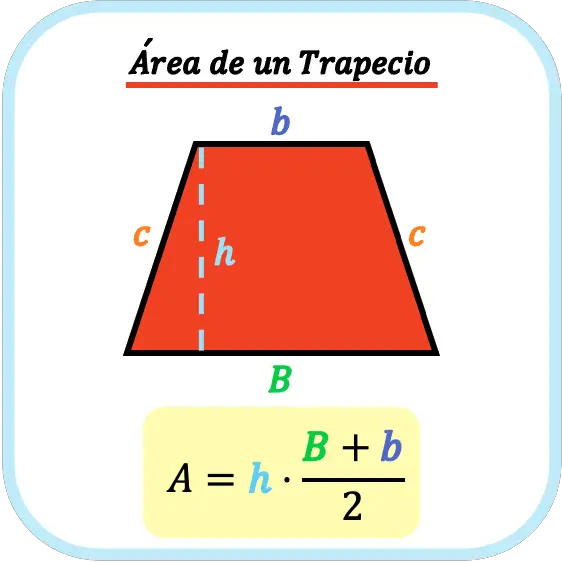
El área de un trapecio es igual a la suma de las bases del trapecio por su altura partido por dos. Por lo tanto, para calcular el área de un trapecio primero se deben sumar sus bases, luego multiplicar por su altura y, por último, dividir entre dos.
De modo que la fórmula para calcular el área de un trapecio es la siguiente:
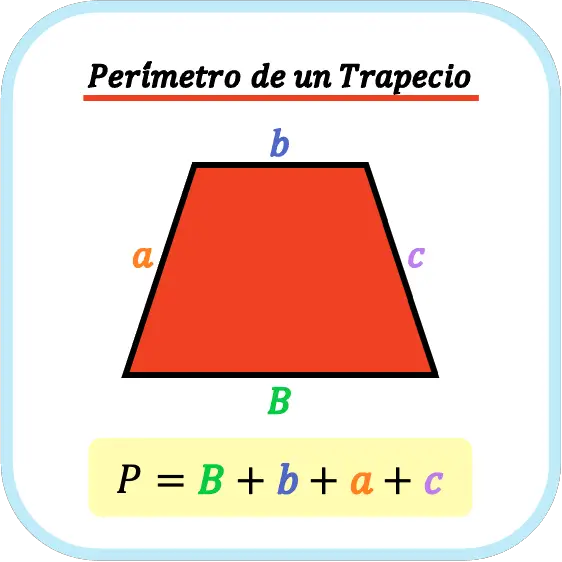
El perímetro de un trapecio es igual a la suma de sus cuatro lados. Por lo tanto, para calcular el perímetro de un trapecio se deben sumar las longitudes de sus dos bases y de sus dos lados oblicuos.
Así pues, la fórmula para calcular el perímetro de un trapecio es la siguiente:
Ten en cuenta que el trapecio isósceles es un tipo de trapecio que tiene los dos lados oblicuos iguales. De modo que si el trapecio es isósceles, su perímetro es equivalente a la suma de las bases más dos veces la longitud de un lado oblicuo.
Área y perímetro de un romboide
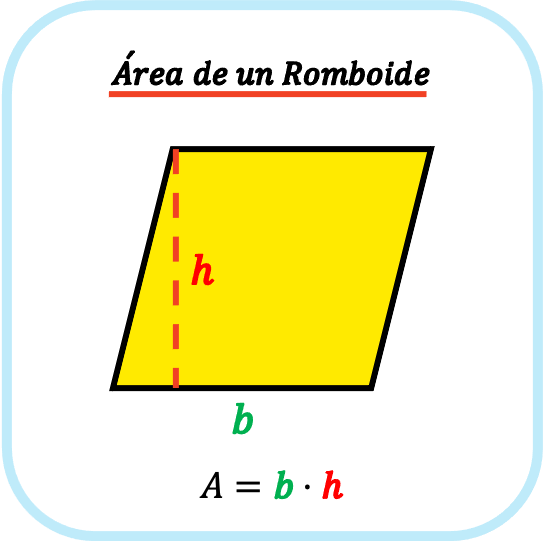
El área de un romboide es igual a la base del romboide por la altura del romboide. Por lo tanto, la fórmula del área de este tipo de figura plana es la siguiente:
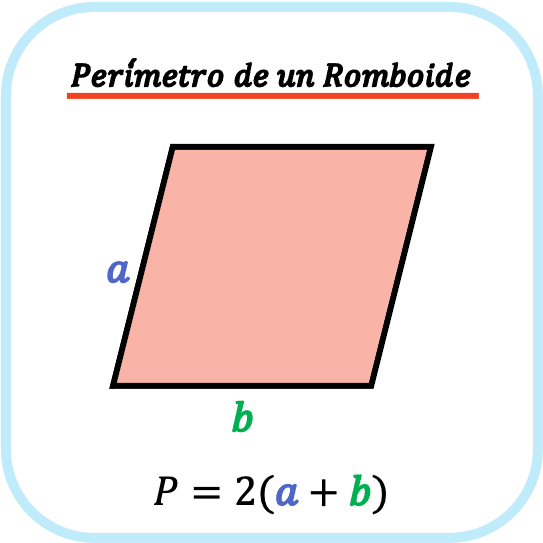
El perímetro de un romboide es la suma de todos sus lados, por tanto, el perímetro de un romboide es igual a la suma de la longitud de la base más la longitud de su lado oblicuo multiplicado por dos.
Área y perímetro de un polígono
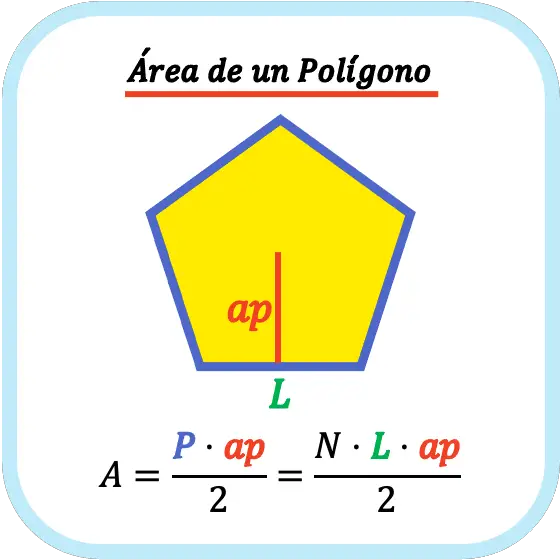
El área de un polígono regular es igual al perímetro por la apotema partido por dos. Por lo tanto, como todos los lados de un polígono regular son iguales, el área de un polígono regular es la longitud de un lado del polígono por el número de lados por la apotema dividido por dos.
Así que la fórmula para calcular el área de un polígono regular es la siguiente:
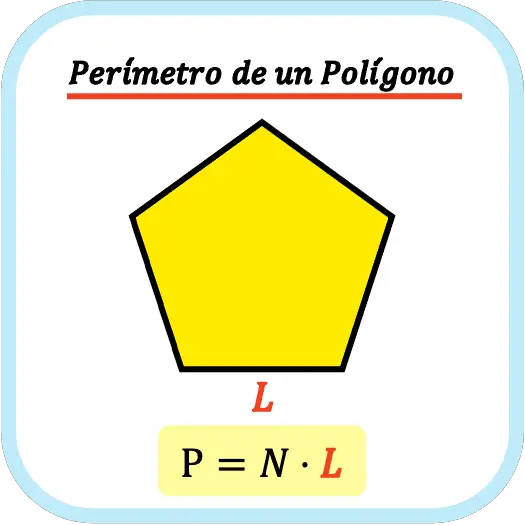
El perímetro de un polígono se calcula sumando las longitudes de todos sus lados. Por lo tanto, el perímetro de un polígono regular es igual al número de lados del polígono por la longitud de unos de sus lados.
De modo que la fórmula para calcular el perímetro de un polígono regular es la siguiente:
Área y perímetro de un círculo
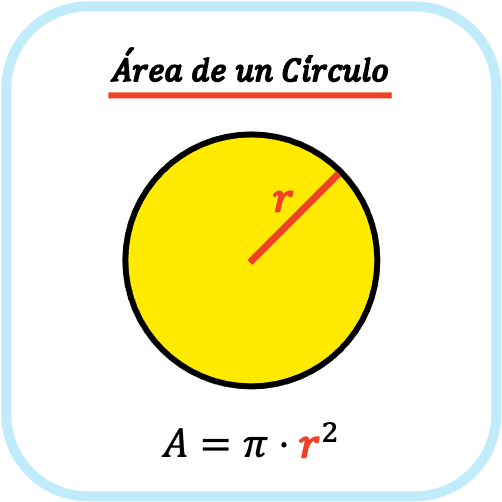
El área de un círculo es igual al número pi por el radio del círculo al cuadrado. Por lo tanto, para calcular el área de un círculo debemos elevar su radio al cuadrado y luego multiplicarlo por la longitud del radio del círculo.
Es decir, la fórmula del área de una figura circular es la siguiente:
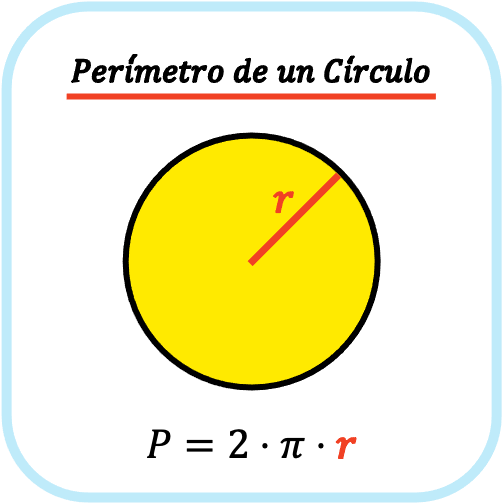
El perímetro de un círculo es igual a dos por el número pi por el radio del círculo. Por lo tanto, para calcular el perímetro de un círculo se debe multiplicar su radio por dos por el número pi.
En definitiva, la fórmula para calcular el perímetro de un círculo es la siguiente:
Área y perímetro de un sector circular
El área de un sector circular es igual al número pi por el radio del sector circular al cuadrado por el ángulo del sector circular (en grados) dividido por 360.
Así que la fórmula para calcular el área de un sector circular es la siguiente:
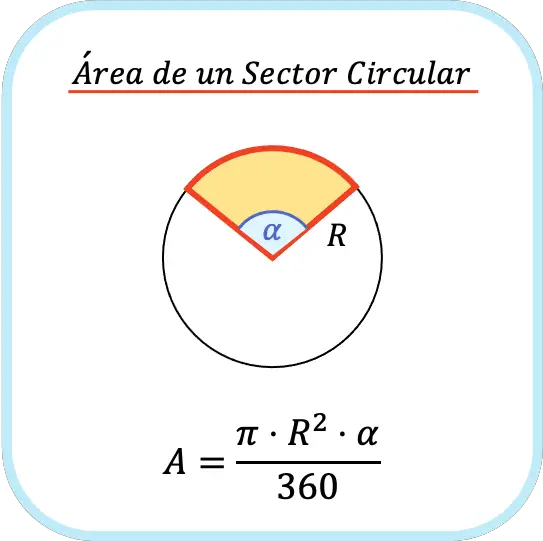
Ten en cuenta que esta fórmula solo puede utilizarse si el ángulo está en grados. Cuando el ángulo está expresado en radianes tienes dos opciones para hacer el cálculo del área de un sector circular: pasar el ángulo a grados y aplicar la fórmula anterior, o usar directamente la siguiente fórmula:
El perímetro de un sector circular es igual a la suma de los lados del sector circular (que son los radios de la circunferencia) más la longitud del arco del sector circular.
Así que para sacar el perímetro de un sector circular debemos multiplicar por dos el radio de la circunferencia en la que está inscrito y luego sumar el arco de la figura circular.
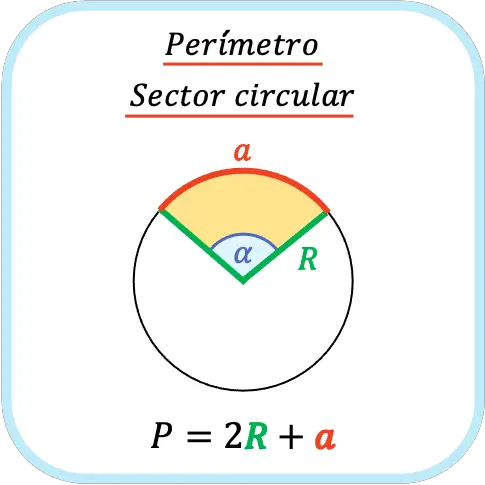
Ten presente que la longitud del arco de un sector circular se calcula aplicando la fórmula del perímetro de un círculo, ya que en realidad el arco es la parte proporcional al ángulo del sector circular de todo el perímetro del círculo.
Área y perímetro de una corona circular
El área de una corona circular es el área del círculo mayor menos el área del círculo menor. Por lo tanto, el área de una corona circular es igual a pi por la diferencia de los cuadrados de los radios de la corona circular.
En definitiva, la fórmula para calcular el área de una corona circular es la siguiente:
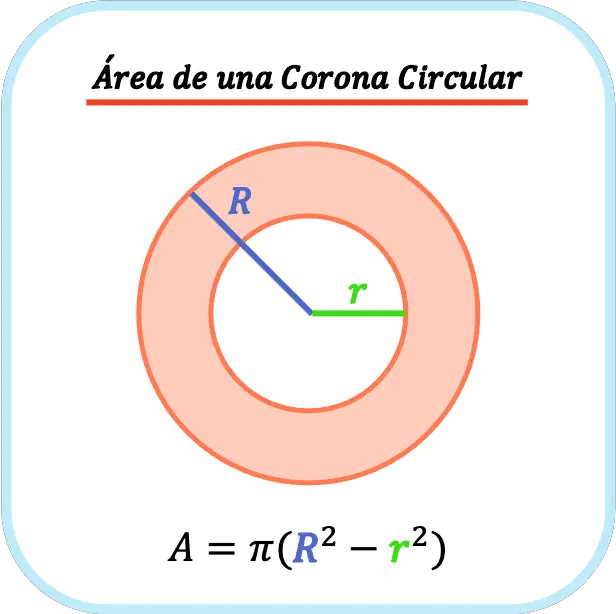
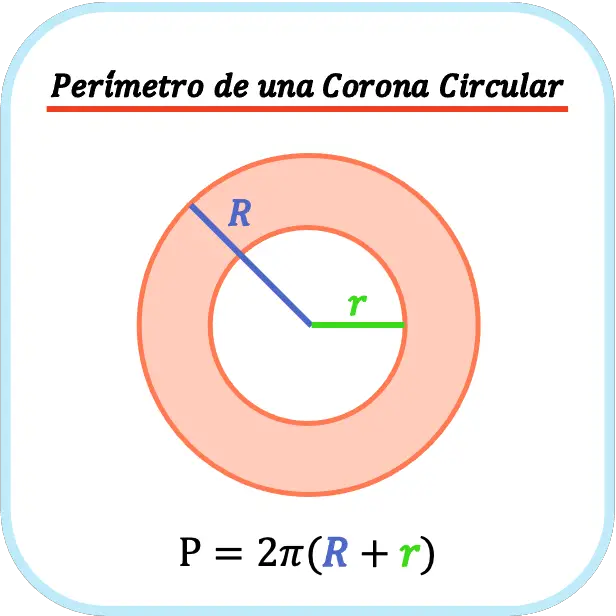
El perímetro de una corona circular es la suma de su perímetro exterior más su perímetro interior. Por lo tanto, el perímetro de una corona circular es igual a dos por pi por la suma de su radio exterior más su radio interior.
En definitiva, la fórmula para calcular el perímetro de una corona circular es la siguiente:
Área y perímetro de un trapecio circular
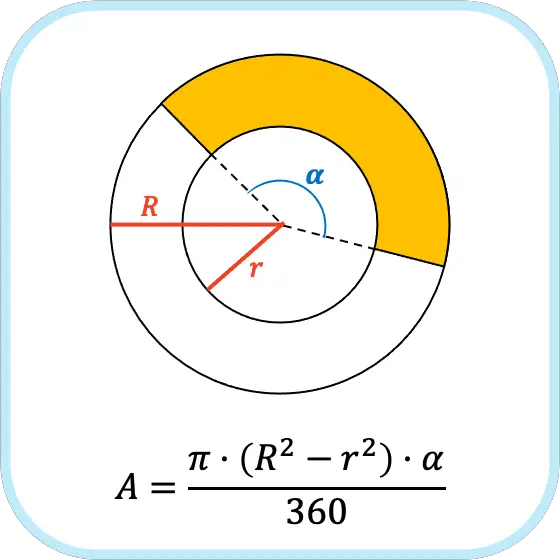
Para calcular el área de un trapecio circular se debe restar el área del sector circular menor al área del sector circular mayor. Por lo tanto, el área de un trapecio circular es igual al producto del número pi por la diferencia de los cuadrados de los radios de la corona circular por la proporción del ángulo del trapecio circular.
De manera que la fórmula del área de este tipo de figura circular es la siguiente:
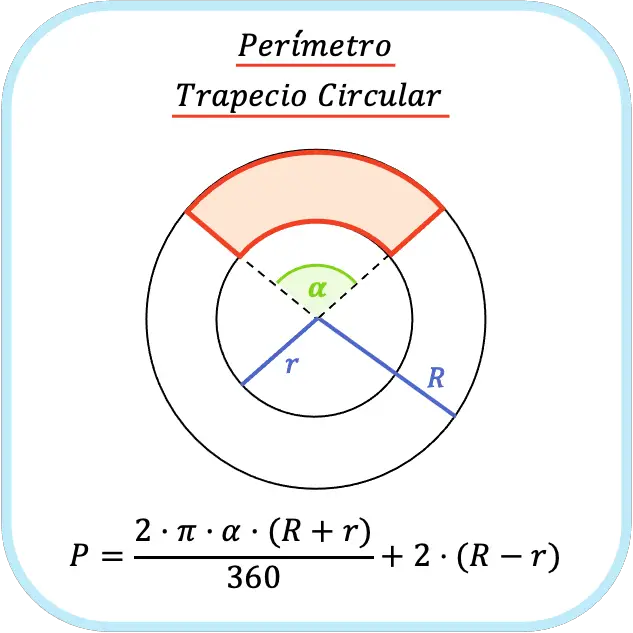
El perímetro de un trapecio circular es igual a la suma de la longitud del arco exterior más la longitud del arco interior más dos veces la diferencia de los dos radios.
Por lo tanto, la fórmula que debes utilizar para determinar el perímetro de un trapecio circular es la siguiente:
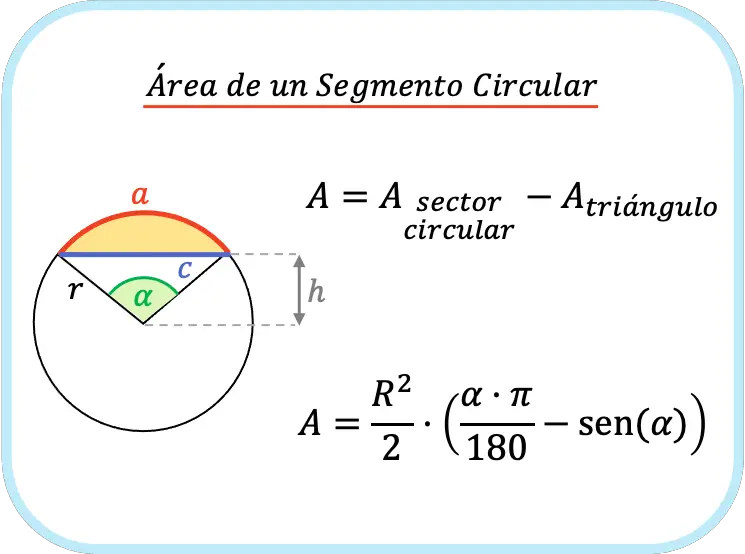
Área y perímetro de un segmento circular
El área de un segmento circular es igual al área del sector circular menos el área del triángulo. Por tanto, la fórmula para calcular el área de un segmento circular es un medio por el radio del segmento circular al cuadrado por la diferencia del ángulo y el seno del ángulo del segmento circular.
El perímetro de un segmento circular es la suma de la cuerda más el arco que limitan el segmento circular. Por lo tanto, para calcular el perímetro de un segmento circular se debe sumar la longitud de la cuerda y la longitud del arco.
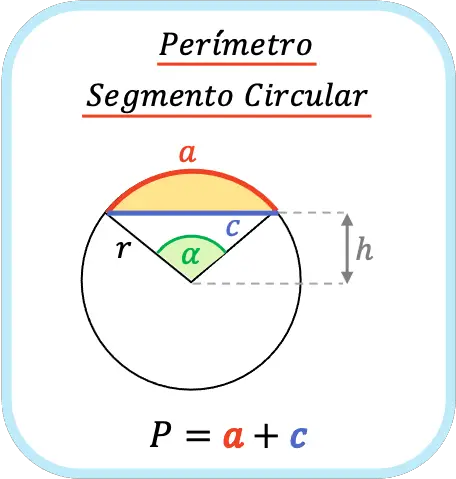
La longitud del arco de un segmento circular se puede encontrar fácilmente utilizando la siguiente fórmula:
Sin embargo, para hallar la longitud de la cuerda del segmento circular debemos utilizar la razón trigonométrica del seno. De manera que la longitud de la cuerda de un segmento circular es igual a 2 por el radio de la circunferencia por el seno de la mitad del ángulo:
Por lo tanto, la fórmula del perímetro de un segmento circular es la suma de las dos expresiones anteriores:
Ten en cuenta que para usar esta fórmula el ángulo debe estar en grados, por lo que si tienes el ángulo en radianes primero debes pasarlo a grados.
