En este post te explicamos cómo se calcula el área de un trapecio isósceles. Podrás ver varios ejemplos resueltos de áreas de trapecios isósceles y, además, podrás calcular el área de cualquier trapecio isósceles con la calculadora online que hay al final.
Índice
Fórmula del área de un trapecio isósceles
El área de un trapecio isósceles es igual a la altura del trapecio isósceles por la suma de las bases del trapecio isósceles dividido entre dos.
Es decir, la fórmula para calcular el área de un trapecio isósceles es la siguiente:
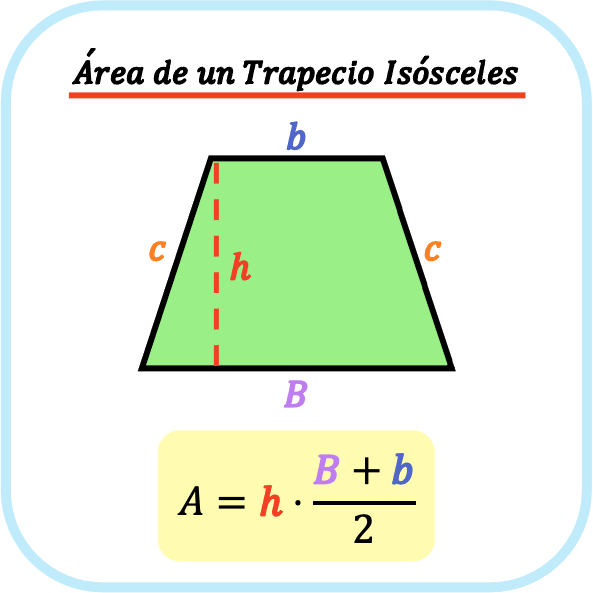
👉 Puedes usar la calculadora que hay más abajo para calcular el área de cualquier trapecio isósceles.
Normalmente, la altura del trapecio isósceles no la sabemos directamente, sino que debemos encontrarla con el teorema de Pitágoras. Por lo tanto, para calcular la superficie de un trapecio isósceles primero tendremos que hallar su altura y luego aplicar su fórmula correspondiente.
En realidad, al sumar las dos bases del trapecio isósceles y luego dividir entre dos estamos calculando una media de las longitudes de las bases, por lo que la superficie de un trapecio isósceles es equivalente a su altura por la media de sus bases.
Ejemplo del área de un trapecio isósceles
Ahora que ya sabemos cuál es la fórmula del área de un trapecio isósceles, a continuación tienes un ejemplo resuelto del área de un trapecio de este tipo para que veas cómo se saca el área de un trapecio isósceles.
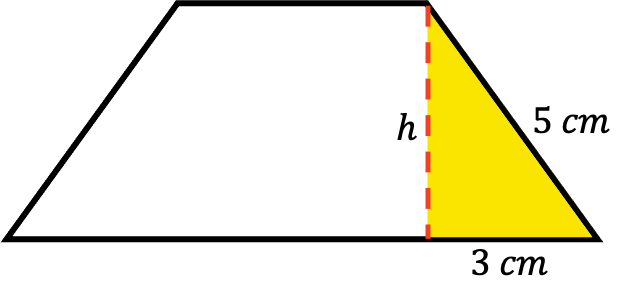
- Calcula el área del siguiente trapecio isósceles:

En este caso no sabemos la altura de la figura plana, por lo tanto, para hallar el área del trapecio isósceles primero tenemos que determinar su altura y luego aplicar la fórmula vista más arriba.
Entonces, para obtener la altura del trapecio isósceles debemos emplear el teorema de Pitágoras con uno de los triángulos rectángulos inscritos:
Una vez ya conocemos la altura del cuadrilátero, simplemente debemos utilizar la fórmula de la superficie de un trapecio isósceles:
Ahora sustituimos los datos en la fórmula y hacemos el cálculo del área del trapecio isósceles:
Calculadora del área y del perímetro de un trapecio isósceles
Introduce las longitudes de las bases y de los lados oblicuos del trapecio isósceles en la siguiente calculadora para calcular el área y el perímetro del trapecio isósceles de manera online.
La letra se refiere a la base mayor del trapecio isósceles,
a la base pequeña y
a su lado repetido. Debes introducir los números en centímetros utilizando el punto como separador decimal.
Área de un trapecio isósceles sin su altura
Aunque es poco usual, también se puede sacar el área de un trapecio isósceles sin saber cuánto es su altura. Para ello, debemos usar una expresión matemática llamada fórmula de Brahmagupta.
La fórmula de Brahmagupta establece que para calcular el área de un trapecio isósceles sin saber su altura se debe hacer la raíz cuadrada del producto de las diferencias entre el semiperímetro del trapecio isósceles y las longitudes de cada lado de la figura.
Donde es la base mayor del trapecio,
la base menor,
el lado repetido y
es el semiperímetro, que se calcula con la siguiente fórmula:
La fórmula de Brahmagupta es análoga a la fórmula de Herón para los triángulos.
Para que veas cómo se hace, te dejamos con un ejercicio resuelto del área de un trapecio isósceles. En este caso, calcularemos el área del mismo trapecio que en el ejemplo de arriba pero sin hallar su altura.

En primer lugar, calculamos el semiperímetro del trapecio isósceles:
Y luego aplicamos la fórmula de Brahmagupta para determinar el área del trapecio isósceles:

