Aquí veremos qué és y cómo se calcula el área de un trapecio circular. Además, encontrarás ejercicios resueltos sobre el área del trapecio circular.
Índice
Cómo calcular el área de un trapecio circular
Para calcular el área de un trapecio circular se debe restar el área del sector circular menor al área del sector circular mayor. Por lo tanto, el área de un trapecio circular es igual al producto del número pi por la diferencia de los cuadrados de los radios de la corona circular por la proporción del ángulo del trapecio circular.
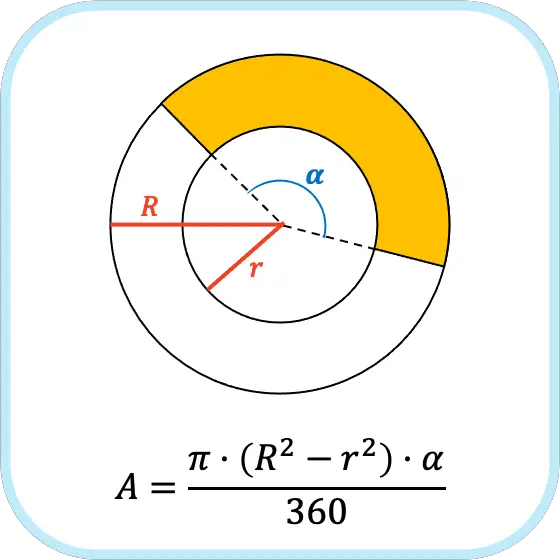
Esta fórmula se utiliza para calcular el área de un trapecio circular cuando el ángulo está expresado en grados. Pero si el ángulo del trapecio circular está expresado en radianes debes cambiar el 360 por 2π.
Ejemplo del área de un trapecio circular
Una vez hemos visto cuál es la fórmula del área de un trapecio circular, vamos a resolver un ejemplo paso a paso para que puedas ver cómo se encuentra el área de un trapecio circular.
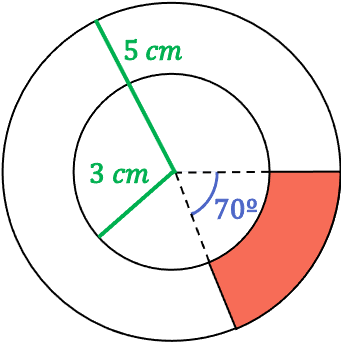
Como hemos visto en su definición, la fórmula para determinar el área del trapecio circular es la siguiente:
En este caso ya sabemos cuánto es el radio exterior y el radio interior de la corona circular y, además, conocemos el ángulo que del trapecio circular. De modo que simplemente tenemos que sustituir los datos proporcionados en la fórmula para hallar el área:
Ejercicios resueltos de áreas de trapecios circulares
Ejercicio 1
Calcula el área sombreada del trapecio circular:
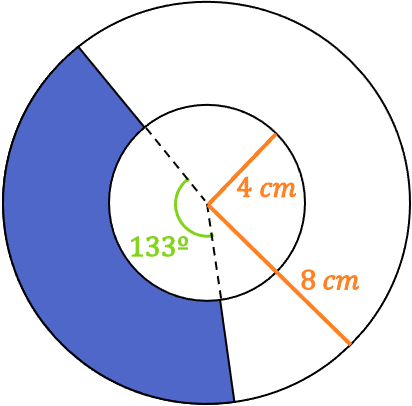
Para hallar el área del trapecio circular debemos utilizar su fórmula correspondiente:
Ahora sustituimos los valores del trapecio circular en la fórmula y calculamos su área:
Ejercicio 2
Determina el ángulo del trapecio circular cuya área es 300 cm2 cuyos radios son 9 cm y 15 cm.
Para resolver este problema del área de un trapecio circular debemos aplicar la fórmula que sirve para determinar su área:
Ahora sustituimos los datos del problema en la fórmula:
Y despejamos el ángulo de la ecuación anterior para hallar su valor:

