Aquí te explicamos cómo sacar el área de un hexágono con ejemplos. También podrás calcular el área y el perímetro de cualquier hexágono con la calculadora que hay al final.
Índice
Cómo calcular el área de un hexágono
El área de un hexágono es igual al perímetro del hexágono por su apotema partido por dos. Por lo tanto, el área de un hexágono regular es tres por la longitud de uno de sus lados por su apotema.
De modo que la fórmula del área de un hexágono regular es la siguiente:
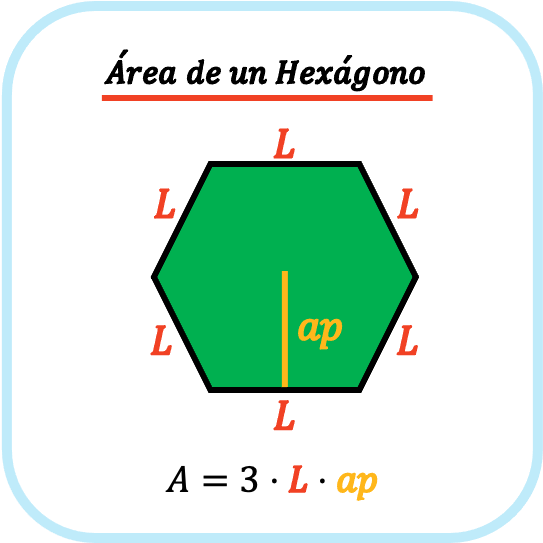
👉 Puedes usar la calculadora que hay más abajo para calcular el área de cualquier hexágono regular.
La fórmula del área de un hexágono regular se puede demostrar fácilmente, ya que un hexágono de este tipo tiene seis lados iguales y, por tanto, su perímetro es seis veces la longitud de un lado.
Por otro lado, un hexágono regular se puede descomponer en seis triángulos idénticos de ángulo 60º, por lo que el apotema de un hexágono regular se puede hallar utilizando la siguiente fórmula:
De modo que el área de un hexágono también se puede sacar conociendo solo su lado, ya que el área de un hexágono regular es igual a tres por la raíz de tres por el lado del hexágono al cuadrado dividido entre dos.
Lógicamente, para determinar el área de un hexágono no hace falta que memorices todas las fórmulas que hemos deducido, con utilizar solo una es suficiente.
Ejemplo del área de un hexágono
Una vez sabemos cuál es la fórmula del área de un hexágono regular, en este apartado calcularemos el área de un polígono de este tipo a modo de ejemplo.
- Calcula el área del hexágono regular cuyo lado mide 8 cm.
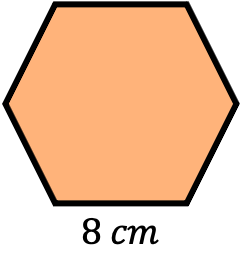
En este caso únicamente conocemos el lado del hexágono, así que podríamos aplicar la fórmula del área de un hexágono sabiendo solo su lado. Sin embargo, en este caso resolveremos el ejercicio utilizando el teorema de Pitágoras para que veas las dos opciones posibles.
Una característica particular de los hexágonos regulares es que su radio mide lo mismo que su lado, por lo tanto, podemos aplicar el teorema de Pitágoras con el siguiente triángulo equilátero para calcular la apotema del polígono:
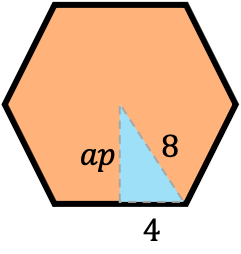
De manera que solo nos queda utilizar la fórmula del área de un hexágono regular y hacer el cálculo:
Como puedes comprobar, si utilizamos la fórmula en la que solamente necesitamos sustituir la longitud del lado, obtenemos el mismo resultado:
Calculadora del área y perímetro de un hexágono
Introduce la longitud del lado o de la apotema en la siguiente calculadora para sacar el área y el perímetro del hexágono.
Debes seleccionar si pondrás la longitud del lado o de la apotema e introducir el número en centímetros utilizando el punto como separador decimal.
Área de un hexágono irregular
Para calcular el área de un hexágono irregular no se puede utilizar la misma fórmula del hexágono regular, sino que se debe dividir el hexágono en triángulos y sacar el área de cada triángulo. A este proceso se le llama triangulación de un hexágono.
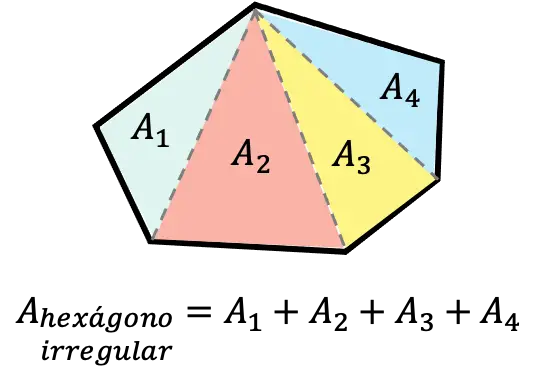
En este caso hemos representado estos cuatro triángulos, pero se puede dividir el polígono irregular en los triángulos que más convengan. Recuerda que el área de un triángulo es la longitud de su base por su altura dividido entre dos.
De este modo se descompone el hexágono irregular en triángulos más pequeños y encontrar su área total resulta mucho más sencillo.
